Caso práctico
Un director de marketing quiere cuantificar el efecto de los gastos en publicidad y la renta de los consumidores sobre las ventas de su empresa. Con este objetivo, recoge datos para las variables ‘Ventas’ —V—, ‘Renta de los consumidores’ —R— y ‘Gastos en publicidad’ —GP— de sus 10 delegaciones y plantea un modelo de regresión lineal:
V_{t} = \beta_{0} + \beta_{1} R_{t} + \beta_2 GP_{t} + \varepsilon_{t}
que estima por mínimos cuadrados ordinarios.
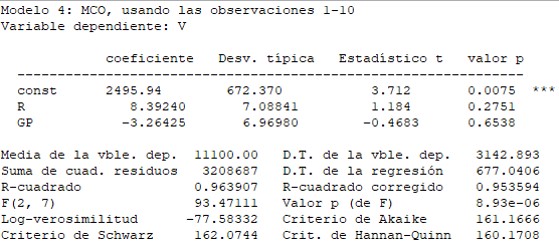
Los resultados obtenidos lo desconciertan:
- Ninguna de las variables explicativas resultan individualmente relevantes:
Prob(t_1) = 0,2571
Prob(t_2) = 0,6538 - La estimación del parámetro \beta_2 indica la existencia de una relación inversa entre las ventas y los gastos en publicidad cuando, a priori, esperaba una relación directa.
- La regresión explica aproximadamente el 96% de las variaciones muestrales de la variable ‘Ventas‘.
- A pesar de que las variables ‘Renta‘ y ‘Gastos en Publicidad’ no se muestran individualmente relevantes, sí lo son conjuntamente, prácticamente a cualquier nivel de significación: Prob(F) = 8,93E-06.
- Ninguna de las variables explicativas resultan individualmente relevantes:
Decide, entonces, estimar dos regresiones simples. En la primera, emplea únicamente como variable explicativa la renta de los consumidores y, en la segunda, los gastos en publicidad:
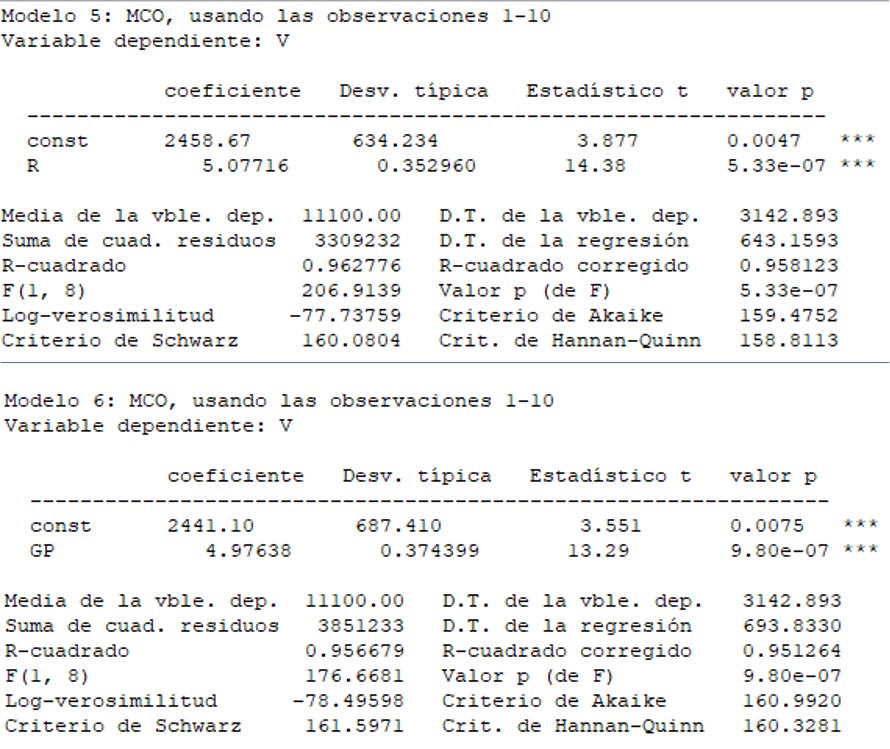
En ambos casos, las variables explicativas son individualmente relevantes —prácticamente a cualquier nivel de significación— y el signo de b_1 en la segunda regresión es positivo, tal como cabía esperar.
Este ejemplo muestra las consecuencias que puede tener incluir en un modelo dos variables explicativas altamente colineales —r_{R,GP} = 0,998—. En este caso, los estimadores MCO, tienen varianzas muy elevadas, lo que complica la inferencia. El modelo inicialmente planteado tiene un elevado grado de multicolinealidad.
Multicolinealidad
Concepto
- Multicolinealidad perfecta: si entre los regresores existen relaciones lineales exactas.
- Ortogonalidad: supone la ausencia de relación lineal entre los regresores incluidos en la ecuación del modelo.
- Multicolinealidad imperfecta: consiste en la existencia de una relación lineal aproximada entre los regresores.
La multicolinealidad perfecta es una situación muy poco frecuente en las aplicaciones empíricas en tanto en cuanto, desde un punto de vista lógico, carece de sentido incorporar a un modelo dos variables que suministran la misma información para explicar el comportamiento del regresando.
En este caso, el rango de la matriz de observaciones de los regresores no es pleno y, por tanto, no es posible obtener el vector de estimadores MCO. Los EMCO(b) son indeterminados y sus varianzas infinitas.
La ortogonalidad también es una situación más teórica que real porque raramente se da en la práctica. En general, los regresores de la ecuación son variables económicas, que son más o menos multicolineales, de manera que —aunque entre ellos no existan relaciones lineales exactas— sí pueden existir relaciones lineales más o menos intensas.
La multicolinealidad imperfecta es muy común en la práctica econométrica y no supone el incumplimiento de ninguna de las hipótesis del MRLNC. Por tanto, los EMCO(b) están determinados y son los mejores estimadores que pueden obtenerse porque conservan todas sus buenas propiedades estadísticas. Sin embargo, pueden no ser buenos estimadores debido a las consecuencias que pueden derivarse de la existencia de relaciones lineales intensas entre algunos de los regresores del modelo.
Multicolinealidad imperfecta
Los regresores están, prácticamente siempre, más o menos correlacionados, de manera que en la inmensa mayoría de las aplicaciones empíricas existe multicolinealidad imperfecta. La distinción importante no es entre presencia y ausencia de multicolinealidad, sino si esta ocasiona un problema.
La aparición del problema, habitualmente, está relacionado con la inclusión en el modelo de regresores que:
- Mantienen relaciones de causalidad.
Esto es lo que sucede si, por ejemplo, tratamos de explicar el gasto en calefacción de los hogares españoles en función del número de miembros y del tamaño de sus viviendas sin considerar que el tamaño de las viviendas, a su vez, es función del número de miembros de las familias. O si se incluye en el modelo una misma variable actual y retardada porque las variables económicas suelen estar muy correlacionadas con sus valores pasados.
- Están relacionados por casualidad.
Entre ellos no existe una relación teórica de causa y efecto sino que ambos están relacionados con una tercera variable y es por eso por lo que están relacionados entre sí. Esta situación es muy frecuente en los modelos temporales, porque muchas variables económicas siguen líneas de tendencia comunes.
Por ejemplo, si tomamos datos de periodicidad inferior a un año de la superficie forestal quemada y del empleo en la hostelería, habitualmente, encontraremos una elevada correlación positiva entre estas dos variables porque sus valores máximos y mínimos se encuentran en los mismos trimestres del año. Su relación es casual y se debe a la existencia de una tendencia común.
Otro ejemplo muy ilustrativo es la clara relación, que según se aprecia en el gráfico, existe entre el número de nacimientos y los nidos de cigüeña: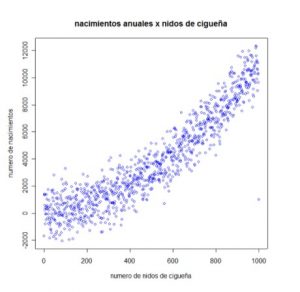 ocasionada —tal como se indica en la página web de la Unidad de Análisis Estadístico del CSIC — a su dependencia, entre otros factores, de la extensión de la localidad.
ocasionada —tal como se indica en la página web de la Unidad de Análisis Estadístico del CSIC — a su dependencia, entre otros factores, de la extensión de la localidad. - Se mantienen aproximadamente constantes a lo largo de la muestra en un modelo con ordenada en el origen.
Cuando los valores de algún regresor se sitúan próximos al valor de su media en la muestra, sus observaciones son aproximadamente proporcionales a las del regresor ficticio.
Esta situación puede darse, por ejemplo, si se estima un modelo —con ordenada en el origen— explicativo del consumo de los hogares en función de sus ingresos y del tamaño de las familias con una muestra atemporal para las diferentes regiones de un país desarrollado. En este caso, es probable que la variable ‘tamaño de las familias’ presente una escasa variabilidad a lo largo de la muestra.
- Mantienen relaciones de causalidad.
Las consecuencias que se derivan de la existencia de relaciones lineales intensas entre algunos de los regresores del modelo son:
- Varianzas grandes de los estimadores
El hecho de que la varianza de estos estimadores sea mínima entre los de su clase —estimadores lineales e insesgados— no implica que, necesariamente, sea pequeña y una varianza grande significa un estimador menos preciso.
- Varianzas grandes de los estimadores
\Large \sigma^{2}_{b_i} =\sigma^{2} x^{ii} =\frac{ \sigma^{2}}{\sum_{t=1}^T (x_{it} – \overline{x_i})^2 \times (1-R^2_i)}
depende de:
▬ la varianza de la perturbación que es desconocida y, por hipótesis del MRLNC, constante (hipótesis de homocedasticidad).
▬ la variación a lo largo de la muestra de la variable a la que acompaña \sum_{t=1}^T (x_{it} – \overline{x_i})^2 . Cuanto mayor es la variación total de x_i en la muestra, menor es la varianza del estimador al que acompaña. Matemáticamente, a medida que la variación muestral de x_i se aproxima a cero, la varianza del estimador se aproxima a infinito.
▬ del valor del coeficiente de determinación de la regresión que explica el comportamiento de la variable x_i en función de los restantes regresores del modelo, que denotaremos por R^2_i. Cuanto mayor sea el grado de multicolinealidad, mayor es el valor de R^2_i y, por tanto, mayor es la varianza del estimador.
Si las varianzas estimadas de los estimadores — S^{2}_{b_{i}} — son elevadas:
▬ los intervalos de confianza definidos para los parámetros serán amplios:
IC_{(1- \alpha)} (\beta_{i}) = (b_{i} – t^{\alpha/2}_{T-k-1} S_{b_{i}}; b_{i} + t^{\alpha/2}_{T-k-1} S_{b_{i}})
▬ los estadísticos t_{i} que se utilizan para contrastar la hipótesis de nulidad individual de los parámetros — \lvert t_{i} \lvert = \lvert \frac {b_{i}}{S_{b_{i}}} \lvert — serán pequeños.
Estas circunstancias favorecen la decisión de no rechazo de la hipótesis de nulidad individual de los coeficientes del modelo aún cuando las variables a las que acompañan sean relevantes.
Es bastante habitual que, aunque las variables explicativas no se muestren individualmente relevantes, la hipótesis de nulidad conjunta de los coeficientes angulares se rechace a niveles de significación muy reducidos.
- Inestabilidad de los estimadores y de sus desviaciones típicas estimadas ante pequeñas variaciones muestrales.
Puede suceder que pequeñas variaciones muestrales generen variaciones importantes en los valores de los estimadores MCO y de sus desviaciones típicas estimadas.
- Posibilidad de que los estimadores tengan signos contrarios a los que teóricamente les correspondan.
- Dificultad para interpretar los coeficientes \beta y, por tanto, sus estimaciones.
Los coeficientes estimados —b_{i}— se interpretan como el cambio que, por término medio, se estima que se produce en la variable explicada al variar el regresor x_{i} en una unidad, permaneciendo constantes el resto de las variables explicativas. Sin embargo, cuando existe multicolinealidad imperfecta no es posible aislar el efecto de cada una de ellas sobre el regresando porque no se puede suponer que el resto de las explicativas permanecen constantes —ya que entre ellas existen relaciones lineales— .
- Puede no tener efectos negativos sobre la predicción
Para que un modelo proporcione buenas predicciones es necesario que se mantenga estable para alguna observación extramuestral. En caso de multicolinealidad imperfecta, no solo está relacionado el regresando con los regresores, sino que entre los propios regresores existen relaciones lineales aproximadas.
Si además del modelo, también se mantienen estables dichas relaciones, es posible que, a pesar de la multicolinealidad, el modelo tenga una buena capacidad predictiva.
- Inestabilidad de los estimadores y de sus desviaciones típicas estimadas ante pequeñas variaciones muestrales.
Los programas estadísticos y econométricos de uso habitual no indican explícitamente la existencia de multicolinealidad imperfecta. Aunque el grado de dependencia lineal entre los regresores del modelo sea muy elevado, la matriz X^{\prime}X es invertible y, por tanto, se puede estimar por mínimos cuadrados ordinarios.
La multicolinealidad es una característica de las muestras y para analizar si el grado de multicolinealidad existente es lo suficientemente elevado como para ocasionar un problema hay un conjunto de reglas prácticas, más o menos útiles según los casos:
- Análisis de los resultados de la estimación.
Un primer signo de alerta sobre la presencia de multicolinealidad entre los regresores de un modelo, son los resultados de la estimación: modelos fuertemente explicativos —coeficiente de determinación alto— , con parámetros no significativos individualmente —varianzas estimadas de los estimadores elevadas— y sí en su conjunto y, posiblemente, con coeficientes estimados que presenten signos inadecuados.
▬ Un valor alto de R^{2} puede relacionarse con un valor pequeño de SCE y, por tanto, con un valor bajo de la varianza estimada de la perturbación (S^{2}).
▬ Si las varianzas estimadas de los estimadores son elevadas puede deberse a la existencia de una relación lineal intensa entre las variables explicativas del modelo.\Large S^{2}_{b_i} = S^{2} x^{ii} =\frac{ S^{2}}{\sum_{t=1}^T (x_{it} – \overline{x_i})^2 \times (1-R^2_i)}
Esta circunstancia no siempre se da en la práctica ya que no todas las variables consideradas tienen por qué estar altamente correlacionadas. En las aplicaciones empíricas es bastante habitual que el valor del coeficiente de determinación —R^{2}—sea bastante elevado y algún/os regresor/es no se muestre/n individualmente relevante/s. En este caso, una forma de analizar la capacidad explicativa de la variable no significativa es estimando un modelo de regresión lineal simple en el que ésta sea la única explicativa.
Análisis de los coeficientes de correlación lineal simple entre las variables explicativas.
Valores elevados para los coeficientes de correlación simple (r_{ij}) —cociente entre la covarianza de las variables y el producto de sus desviaciones típicas—, próximos a 1 ó a –1, indican una fuerte relación lineal entre variables, y constituyen un indicio de posibles problemas, aunque no siempre con consecuencias negativas sobre los resultados de la estimación.▬ Aunque \lvert r_{ij} \lvert \eqsim 1 , las varianzas estimadas de los estimadores pueden no ser demasiado elevadas si S^{2} es pequeño y/o la variación muestral de x_{i} es elevada.
▬ Aunque \lvert r_{ij} \lvert \eqsim 0 , las varianzas estimadas de los estimadores pueden ser elevadas si S^{2} es elevado y/o la variación de x_{i} en la muestra no es suficiente.Valores elevados de los coeficientes de correlación lineal simple no implican, necesariamente, altas desviaciones típicas estimadas de los estimadores y valores bajos de estos coeficientes podrían relacionarse con elevadas desviaciones típicas estimadas.
- Cálculo de los coeficientes de determinación de la regresión de cada variable explicativa con los demás regresores de la ecuación.
En el caso de que el modelo tenga más de dos variables explicativas, deben considerase las correlaciones múltiples de cada una con respecto a las demás. Aunque entre pares de variables explicativas apenas exista correlación —lo que implicaría valores pequeños de r_{ij} — alguna de ellas podría estar muy correlacionada con el conjunto de todas las demás. En este caso, el valor del coeficiente de determinación de la regresión de la variable i-ésima con los restantes regresores de la ecuación —R^{2}_{i} — tomaría un elevado valor.
Cuanto mayor sea el valor de R^{2}_{i} , mayor es la varianza del estimador.
- Cálculo del determinante de la matriz de correlación de las variables explicativas.
Los elementos de esta matriz —representada por R_{X} — son los coeficientes de correlación lineal simple entre las variables explicativas del modelo:
R_{X} = \begin{pmatrix} r_{11} & r_{12} & ··· & r_{1k} \\ r_{21} & r_{22} & ··· & r_{2k} \\ ··· & ··· & ··· & ···\\ r_{k1} & r_{k2} & ··· & r_{kk} \end{pmatrix} = \begin{pmatrix} 1 & r_{12} & ··· & r_{1k} \\ r_{21} & 1 & ··· & r_{2k} \\ ··· & ··· & ··· & ···\\ r_{k1} & r_{k2} & ··· & 1 \end{pmatrix}
Es una matriz cuadrada de orden k, simétrica y sus elementos diagonales iguales a la unidad.
El determinante de esta matriz está tanto más próximo a cero, cuanto mayor es el grado de multicolinealidad.
- El análisis del factor de inflación de la varianza (FIV).
Este factor puede interpretarse como la razón entre la varianza estimada de b_{i} y la que le correspondería en el supuesto de que x_{i} no estuviese correlacionada con las restantes explicativas del modelo.
FIV_{i} =\Large \frac {1}{1- R^2_i}
Cuanto más elevado es este cociente, mayor es el grado de multicolinealidad. El principal inconveniente de esta medida es que no hay un criterio estricto para establecer a partir de qué valor indica un problema serio. Algunos autores sugieren que si su valor es superior a 10 —lo que sucede si R^2_i > 0,9 — la correspondiente variable es altamente colineal.
Un FIV alto no es condición necesaria ni suficiente para que las varianzas estimadas de los estimadores tomen un valor elevado.
- Análisis de los resultados de la estimación.
Cuando la multicolinealidad es elevada y tiene importantes consecuencias negativas sobre los resultados de la estimación no existe una única forma de actuar, sino que existen distintas posibles soluciones, dependiendo de la causa que la provoca. Incluso, en algunos casos, puede ser preferible no intentar corregirla y simplemente tenerla en cuenta al interpretar los resultados.
La solución al problema de la multicolinealidad puede resultar poco o nada satisfactoria cuando lo que se pretende es describir y cuantificar la relación existente entre el regresando y los regresores. Entre las alternativas sugeridas con mayor frecuencia están:
- Omitir del modelo la variable causante de la multicolinealidad
Se pueden eliminar regresores cuando su información sea redundante y se vea, claramente, que su efecto está recogido dentro de otra u otras variables. Se puede optar por esta alternativa cuando el coeficiente estimado de la variable, que supuestamente causa colinealidad, tiene un signo contrario al esperado y su supresión no modifica significativamente el ajuste global.
El inconveniente que plantea esta solución es que la omisión de una variable relevante puede causar el incumplimiento de las hipótesis relativas al comportamiento de la perturbación aleatoria, provoca un incremento de la varianza de la perturbación, puede suponer el sesgo y la inconsistencia de los estimadores MCO y hace que aumente la suma de cuadrados de errores.
- Incorporar al modelo una ecuación adicional que recoja la relación causal que existe entre las explicativas
Cuando la multicolinealidad se debe a la existencia de relaciones causales entre las variables explicativas del modelo, esta relación de tipo teórico debe incorporarse al modelo como una ecuación. El nuevo modelo será multiecuacional en lugar de uniecuacional.
- Transformar las variables
▬ Tomar primeras diferencias para todas las variable del modelo.
y_{t} – y_{t-1} = \beta_{1} (x_{1t} – x_{1t-1}) + \beta_{2} (x_{2t} – x_{2t-1}) + ··· + \beta_{k} (x_{kt} – x_{kt-1}) + (\varepsilon_{t} – \varepsilon_{t-1})
Cuando la multicolinealidad se debe a la existencia de tendencias comunes en las variables explicativas, esta transformación puede reducir el grado de colinealidad.
Para interpretar correctamente los resultados, debe tenerse en cuenta que con el modelo transformado —sin ordenada en el origen— se trata de explicar la variación del regresando y que, a su vez, las variables explicativas son las variaciones de las x_{i} originales. Además, si el modelo es clásico, tomar primeras diferencias puede provocar el incumplimiento de la hipótesis de incorrelación de las perturbaciones.
Si la muestra es atemporal, este procedimiento probablemente no es adecuado porque la diferencia entre dos observaciones consecutivas no tiene un significado lógico.
▬ Utilizar cocientes o ratios dividiendo todas las variables del modelo por un factor de escala común como, por ejemplo, la población o un índice de precios.
En este caso, si el modelo original es clásico, la perturbación del modelo transformado —que puede perder la ordenada en el origen— no es homocedástica.
- Aumentar el tamaño de la muestra
Una solución alternativa puede ser la de buscar información adicional que debilite los efectos de la multicolinealidad:
▬ Utilizando datos mixtos de series temporales y de corte transversal
▬ Incorporando nuevos datos que no estén tan afectados por la multicolinealidad.♦ Si la multicolinealidad se debe a que un regresor se mantiene prácticamente constante, al aumentar el tamaño de la muestra es probable que aumente su variabilidad y, por tanto, disminuya el grado de correlación.
♦ Si el problema es consecuencia de que la relación entre las explicativas es casual, un incremento del número de observaciones puede resolver el problema dada la fuerte inestabilidad de este tipo de multicolinealidad.Esta última opción es más teórica que real porque, en general, se trabaja con todos los datos disponibles.
- Convivir con la multicolinealidad.
No intentar corregirla y simplemente tenerla en cuenta para el análisis de los resultados. Esta alternativa está especialmente indicada si:
▬ la variable causante del problema es muy importante desde el punto de vista teórico y su inclusión no provoca problemas muy serios: aunque los estimadores son imprecisos, tienen signos correctos.
▬ el objetivo del modelo es la predicción porque la multicolinealidad no empeora necesariamente la capacidad predictiva del modelo.
- Omitir del modelo la variable causante de la multicolinealidad
Caso práctico: modelo ventas
La relación entre las variables ‘Renta de los consumidores’ y ‘Gastos en Publicidad’ es casual y se debe a que su tendencia es común.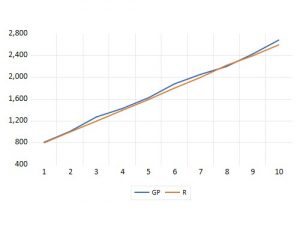
- En los resultados de la estimación hay claros indicios de la existencia de un elevado grado de multicolinealidad:
▬ Las variables explicativas no se muestran individualmente relevantes porque las desviaciones típicas estimadas de los estimadores tienen valores elevados.
▬ El coeficiente de determinación toma un valor elevado.
▬ Las variables explicativas son conjuntamente relevantes, prácticamente a cualquier nivel de significación.
▬ El signo del estimador que acompaña a la variable ‘Gastos en Publicidad’ es contrario a los supuestos teóricos. - El valor del coeficiente de correlación lineal simple está próximo a uno.
r_{GP,R} =\frac {Cov(GP, R)}{S_{GP} \times S_{R}} = 0,998
Entre las variables ‘Gastos en Publicidad’ y ‘Renta’ existe una relación lineal de tipo directo muy intensa.
- El determinante de la matriz de correlación está próximo a cero
R_{X} = \begin{pmatrix} 1 & 0,998 \\ 0,998 & 1 \end{pmatrix} \rightarrow \lvert R_{X} \lvert = 0,04 - El factor de inflación de la varianza es alto.
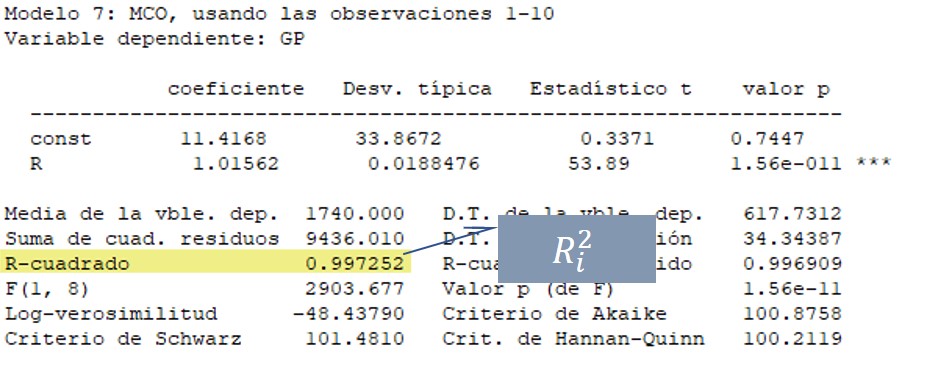
FIV_{i} = \frac {1}{1- 0,997252} = 363,9 > 10
- En los resultados de la estimación hay claros indicios de la existencia de un elevado grado de multicolinealidad:
El analista ha de buscar alguna solución puesto que su objetivo es cuantificar el efecto de las variables ‘Renta de los consumidores’ y ‘Gastos en Publicidad’ sobre las ventas de su empresa.
Al tratarse de datos de corte transversal no es adecuado transformar las variables del modelo tomando primeras diferencias porque la diferencia entre observaciones consecutivas no tiene ningún sentido.
En este caso, una posible solución puede ser ampliar la información muestral con datos mixtos de series temporales y de corte transversal.