Método de Mínimos Cuadrados Ordinarios (MCO)
Estimadores mínimo cuadráticos ordinarios (EMCO)
De los coeficientes \beta
El método de mínimos cuadrados ordinarios (MCO) consiste en elegir la función matemática que proporciona el ajuste de «mínimos cuadrados» a los datos disponibles. O dicho de otra manera, con este método se obtienen los valores aproximados —estimados— de los coeficientes del modelo (\widehat \beta_i = b_i) de tal forma que la función matemática estimada esté lo más próxima posible a los datos observados. Esta proximidad se mide por la suma de los cuadrados de los errores —SCE— que se cometen al estimar los valores de la variable explicada —y_{t}— en función de los valores que toman las variables explicativas — x_{1t}, x_{2t}, ···, x_{kt}—. Estos errores de estimación que se representan por la letra e, se obtienen por diferencia entre el valor observado para la variable explicada ( y_t) y el valor que se estima que va a tomar:
\color{black} e_t = y_t – \widehat y_t
\widehat y_t = b_0 + b_1 x_{1t} + b_2 x_{2t}+ ··· + b_k x_{kt}
Los estimadores de los coeficientes \beta_i que minimizan la suma de los cuadrados de los errores de la estimación —SCE—, se denominan estimadores mínimo cuadráticos ordinarios —EMCO— de \beta_i y se representan por b_i .
La expresión para el cálculo de los EMCO de los parámetros \beta es:
b = (X´X)^{-1} X´Y
Las estimaciones obtenidas en este proceso se utilizan para cuantificar los efectos parciales de las variables explicativas sobre el regresando.
Cálculo matricial
X^{\prime}X= \left(\begin{array}{c}T&\sum_{t=1}^{T}x_{1t}&···&\sum_{t=1}^{T}x_{kt}\\ \sum_{t=1}^{T}x_{1t} & \sum_{t=1}^{T}x_{1t}^{2} & ··· & \sum_{t=1}^{T}x_{1t} x_{kt}\\··· & ··· & ··· & ··· \\ \sum_{t=1}^{T}{x_{kt}} & \sum_{t=1}^{T} x_{kt} x_{1t} & ··· & \sum_{t=1}^{T}x_{kt}^{2}\end{array}\right)
(X^{\prime}X)^{-1} =\frac{1}{|X^{\prime}X|} Adj (X^{\prime}X)^{\prime}= \left(\begin{array}{c}x^{00}&x^{01}&···&x^{0k}\\ x^{10}& x^{11} & ··· & x^{1k}\\··· & ··· & ··· & ··· \\ x^{k0} & x^{k1} & ··· & x^{kk}\end{array}\right)
Para obtener la matriz adjunta de X^{\prime} X debe sustituirse cada uno de sus elementos por su adjunto o cofactor. El adjunto del elemento ij es el valor del determinante que se obtiene al suprimir en la matriz X^{\prime} X la i-ésima fila y la j-ésima columna, multiplicado por el factor (-1)^{ij}.
X^{\prime}Y= \left(\begin{array}{c}\sum_{t=1}^{T}y_{t}\\ \sum_{t=1}^{T}y_{t}x_{1t}\\··· \\ \sum_{t=1}^{T}y_{t}{x_{kt}} \end{array}\right)
Esperanza y varianza de los coeficientes estimados
E(b) = E((X^{\prime}X)^{-1} X^{\prime} \color {red}Y) \color {black}=E((X^{\prime}X)^{-1} X^{\prime} \color {red}(X \beta + \varepsilon) \color {black}) = E((X^{\prime}X)^{-1} X^{\prime} X \beta + (X^{\prime}X)^{-1} X^{\prime} \varepsilon) =E( \beta +(X^{\prime}X)^{-1} X^{\prime} \varepsilon) = \beta +(X^{\prime}X)^{-1} X^{\prime} E (\varepsilon)=\beta
V(b) = E(b -\color{red} E(b)\color{black})(b-\color{red} E(b)\color{black})^{\prime}= E(b -\color{red} \beta \color{black})(b-\color{red} \beta\color{black})^{\prime} = \sigma^2 (X´X)^{-1}
Los elementos diagonales de la matriz de varianzas-covarianzas de los EMCO(b) son las varianzas teóricas de los estimadores ( \sigma^{2}_{b_{i}} = \sigma^{2} x^{ii} ) y los no diagonales las covarianzas teóricas ( \sigma_{b_{i} b_{j}} = \sigma^{2} x^{ij} ).
V(b) = \sigma^2 (X´X)^{-1} = \begin{pmatrix} \color{red} \sigma^2_{b_0} & \sigma_{b_0 b_1} & \sigma_{b_0 b_2} & ··· & \sigma_{b_0 b_k} \\ \sigma_{b_1 b_0} & \color{red} \sigma^2_{b_1} & \sigma_{b_1 b_2} & ··· & \sigma_{b_1 b_k} \\ ··· & ··· & ··· & ··· & ··· \\ \sigma_{b_k b_0} & \sigma_{b_k b_1} & \sigma_{b_k b_2} & ··· & \color{red} \sigma^2_{b_k}\end{pmatrix}
Los elementos de la matriz V(b) son desconocidos porque sus valores dependen de la varianza de la perturbación — \sigma^{2} —, que es un parámetro desconocido, por lo que hay que estimarlos.
De la varianza de la perturbación
La varianza de la perturbación también es un parámetro desconocido — \sigma^{2} — cuyo valor ha de aproximarse en el proceso de estimación. Para estimar la varianza poblacional, habitualmente se calcula la varianza (o la cuasivarianza) muestral, pero en este caso no es posible porque se desconocen los valores que toman las perturbaciones aleatorias. Por esta razón, se recurre a la cuasivarianza muestral de los errores de estimación —e_{t} = y_{t} – \widehat y_{t} — cuyos valores se acercan a los de las perturbaciones en tanto en cuanto, los valores de los estimadores b_{i} se aproximen a los de los parámetros \beta_{i} ya que:
\color{black} \widehat y_{t} \approx E(y_{t})\rightarrow e_{t} = y_t – \widehat y_t \approx \varepsilon_{t} = y_t – E(y_t) .
Para obtener el estimador de la varianza de la perturbación se utiliza la expresión:
\color{black} S^{2} = \frac {SCE}{T – k – 1} = \frac {Y´Y -b´X´Y }{T – k- 1}
A la raíz cuadrada positiva de S^2 se le denomina error estándar de la regresión (standard error of regression).
De las varianzas de los estimadores
Las varianzas teóricas de los estimadores b_i son desconocidas al no conocerse el valor que toma la varianza poblacional de las perturbaciones aleatorias:
\sigma^{2}_{b_i} = \sigma^{2} · x^{ii}
donde x^{ii} son los elementos situados en la diagonal principal de la matriz (X´X)^{-1}
Para estimarlas se sustituye \sigma^{2} por su estimador MCO S^{2} :
S^{2}_{b_i} = S^{2} · x^{ii}
Estas estimaciones se utilizan para medir la precisión, «la confiabilidad» de los EMCO de los parámetros \beta
Los elementos diagonales de la matriz de varianzas-covarianzas de los EMCO(b) son las varianzas estimadas de los estimadores ( S^{2}_{b_{i}} = S^{2} x^{ii} ) y los no diagonales las covarianzas estimadas ( S_{b_{i} b_{j}} = S^{2} x^{ij} ).
\widehat {V}(b) = S^2 (X´X)^{-1} = \begin{pmatrix} \color{red} S^2_{b_0} & S_{b_0 b_1} & S_{b_0 b_2} & ··· & S_{b_0 b_k} \\ S_{b_1 b_0} & \color{red} S^2_{b_1} & S_{b_1 b_2} & ··· & S_{b_1 b_k} \\ ··· & ··· & ··· & ··· & ··· \\ S_{b_k b_0} & S_{b_k b_1} & S_{b_k b_2} & ··· & \color{red} S^2_{b_k}\end{pmatrix}
Muchos programas informáticos, algunos especializados en estadística/econometría —Stata, Eviews, Gretl, R, etcétera— y otros de uso más común, como Excel, incorporan todas las expresiones de cálculo de los estimadores MCO.
Caso práctico: resultados de la estimación MCO del modelo para las ventas
La ecuación estimada del modelo que explica las ventas en función de los precios es:
\color{black} \widehat {V}_t = 164,411 -7,96782 \thinspace PP_t + 3,5303 \thinspace PPC_t
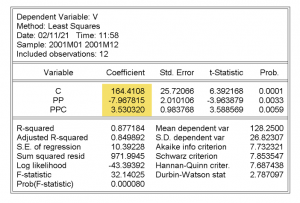
Salida de la estimación MCO del modelo
- En la columna sombreada figuran los valores de los estimadores MCO correspondientes a los coeficientes \beta_i del modelo.
- «Std. Error» son las desviaciones típicas estimadas de los estimadores: S_{b_i} = \sqrt{S^{2} · x^{ii}}
- S.E.of regression —Error estándar de la regresión— es la raíz cuadrada de S^{2}
- Sum squared resid es la suma de cuadrados de errores (SCE)
- Mean dependent var es la media de los valores de la variable explicada —ventas— en la muestra.
- S.D. dependent var es la cuasi-desviación típica muestral del regresando:
S.D. \thinspace dependent \thinspace var = \sqrt{\frac{\sum (y_{t} – \overline y)^{2}}{T – 1}} =\sqrt{\frac{SCT}{T – 1}}= \sqrt{\frac{Y´Y – T · \overline {y}^{2}}{T – 1}}
Salida de la matriz de varianzas-covarianzas estimada de los estimadores
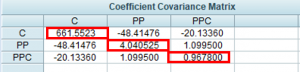Los valores resaltados — elementos diagonales — son las varianzas estimadas de los estimadores ( S^{2}_{b_{i}}=S^{2} · x^{ii})
Los elementos no diagonales son las covarianzas estimadas de los estimadores ( S_{b_{i}b_{j}}=S^{2} · x^{ij} ).
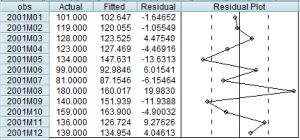
Salida de la tabla de valores observados —‘Actual‘— y estimados —‘Fitted’— del regresando y de los errores de estimación —‘Residual’—
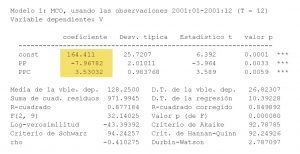
Salida de la estimación MCO del modelo
- En la columna sombreada figuran los valores de los estimadores MCO correspondientes a los coeficientes \beta_i del modelo.
- «Desv. típica» son las desviaciones típicas estimadas de los estimadores: S_{b_i} = \sqrt{S^{2} · x^{ii}}
- D.T. de la regresión —Error estándar de la regresión— es la raíz cuadrada de S^{2}
- Suma de cuad. residuos es la suma de cuadrados de errores (SCE)
- Media de la vble. dep. es la media de los valores de la variable explicada —ventas— en la muestra.
- D.T. de la vble. dep. es la cuasi-desviación típica muestral del regresando:
D. T \thinspace de\thinspace la \thinspace vble. \thinspace dep. = \sqrt{\frac{\sum (y_{t} – \overline y)^{2}}{T – 1}} =\sqrt{\frac{SCT}{T – 1}}= \sqrt{\frac{Y´Y – T · \overline {y}^{2}}{T – 1}}
Salida de la matriz de varianzas-covarianzas estimada de los estimadores
Los valores resaltados — elementos diagonales — son las varianzas estimadas de los estimadores ( S^{2}_{b_{i}}=S^{2} · x^{ii})
Los elementos no diagonales son las covarianzas estimadas de los estimadores ( S_{b_{i}b_{j}}=S^{2} · x^{ij} ).
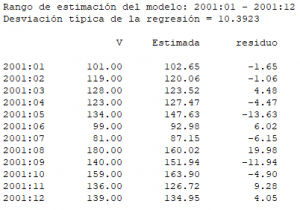
Salida de la tabla de valores observados —‘V‘— y estimados —‘Estimada’— del regresando y de los errores de estimación —‘residuo’—
Salida de la estimación MCO del modelo
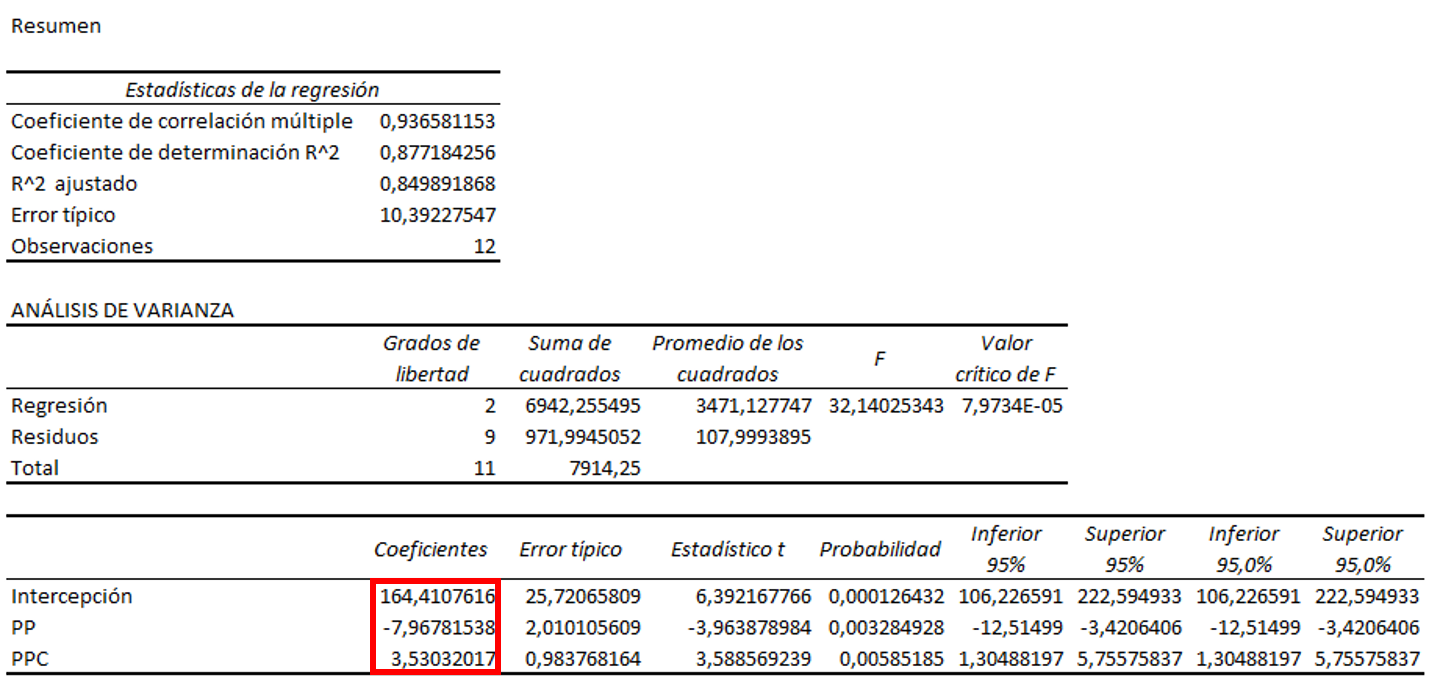
Tabla ‘Resumen’
- Error típico —Error estándar de la regresión— es la raíz cuadrada de S^{2}
Tabla ‘Análisis de la varianza’— columna ‘Suma de cuadrados’
- Total es la suma de cuadrados de totales
SCT = \sum (y_{t} – \overline {y})^{2} =\sum y_{t}^{2}- T \overline {y}^{2} = Y^{\prime}Y – T \overline {y}^{2} - Residuos es la suma de cuadrados de errores (SCE)
- Total es la suma de cuadrados de totales
Última tabla
- En la columna sombreada figuran los valores de los estimadores MCO correspondientes a los coeficientes \beta_i del modelo.
- En la columna «Error típico» figuran las desviaciones típicas estimadas de los estimadores: S_{b_i} = \sqrt{S^{2} · x^{ii}}
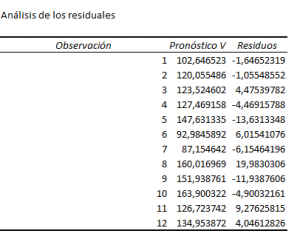
Salida de la tabla de valores estimados del regresando—‘Pronóstico V’— y de los errores de estimación —‘Residuos’—
Un estudio basado en un análisis de regresión, ¿resulta fiable?
¿Cuándo proporciona la regresión un estimador útil del efecto causal? Para que este análisis econométrico resulte útil es necesario que la inferencia estadística sobre el efecto causal sea válida para la población estudiada. En ese caso, se dice que el estudio tiene validez interna.
Esta validez interna depende de que los estimadores MCO gocen de las propiedades deseables desde el punto de vista estadístico (insesgadez, eficiencia, consistencia,…). Si el modelo satisface todas las hipótesis del modelo clásico, los EMCO poseen todas estas propiedades y esto garantiza la validez del procedimiento empleado. En caso contrario, puede que no resulte apropiado emplear este método de estimación y haya que recurrir a procedimientos alternativos.