Caso práctico
Un analista tiene interés en saber cuáles son los principales factores determinantes del beneficio de las empresas. Con tal motivo, reúne la información correspondiente a 50 entidades, solicitándoles, además, los datos de aquellas variables que, en principio, considera determinantes para explicar el beneficio (BN) tales como el número de empleados (NE), la producción (PRO), los recursos propios (RP) y los costes salariales(CS). El beneficio, los recursos propios y los costes salariales están expresados en miles de euros; la producción en unidades físicas y los empleados, en número de personas.
Como punto de partida, especifica un modelo lineal:
BN_t = \beta_0 + \beta_1 NE_t + \beta_2 PRO_t + \beta_3 RP_t + \beta_4 CS_t + \varepsilon_t
lo estima por mínimos cuadrados ordinarios, obteniendo el resultado siguiente:

Una vez finalizado el proceso de estimación, uno de los directivos le pregunta si realmente el número de empleados puede considerarse un factor determinante de los beneficios. El problema es que el analista solamente dispone de la evidencia muestral (los datos) pero el directivo le plantea una cuestión relativa al valor de un parámetro poblacional (\beta_1) de magnitud desconocida.
Para solucionar esta cuestión el analista, en primer lugar, ha de tener claro si es posible inferir los resultados que ha obtenido con esta muestra a la población de referencia. La respuesta es afirmativa siempre y cuando haya verificado que el modelo es clásico, en cuyo caso, los estimadores obtenidos poseen todas las propiedades estadísticas deseables y, por tanto, el modelo tiene validez interna.
En segundo lugar, ha de plantear una suposición sobre el valor de un parámetro desconocido (\beta_1) y comprobar si, con los datos disponibles, puede asumirla como correcta o si, por el contrario, la evidencia muestral la contradice y, para tomar esta decisión, ha de realizar un contraste de hipótesis.
Este directivo, en realidad, lo que le pregunta al analista es si sería posible asumir una restricción de nulidad para el parámetro \beta_1, es decir, si podría considerarse que al variar el número de empleados, manteniéndose constante las restantes variables explicativas consideradas, el beneficio de las empresas no cambia. Podrían establecerse también otro tipo de restricciones tanto referidas a un solo parámetro (¿podría asumirse que, manteniéndose constantes las restantes variables explicativas, por cada unidad producida el beneficio de las empresas aumenta en 200 euros?); como a un subconjunto de parámetros (¿son conjuntamente relevantes el número de empleados y los costes salariales?) o a una combinación lineal de parámetros (¿puede asumirse que los valores de los parámetros que acompañan a las variables producción y recursos propios son de la misma magnitud?).
Para comprobar si la restricción impuesta al parámetro es o no asumible en base a la información muestral, se plantea la restricción establecida como hipótesis nula (H_0) que se enfrenta a la que se denomina hipótesis alternativa (H_1) y se realiza el contraste empleando el estadístico de prueba más apropiado en cada caso.
Cuestiones previas
Procedimiento
- Formulación de las hipótesis nula (H_0) – supuesto en el que se establece la o las restricciones de los parámetros – y la alternativa (H_1).
- Selección y cálculo del valor en la muestra de un estadístico de prueba apropiado que siga una distribución de probabilidad conocida.
- Regla de decisión: el valor del estadístico en la muestra se emplea para tomar una decisión con respecto a la hipótesis nula planteada.
Para decidir, en base a la información muestral disponible, si puede asumirse la hipótesis nula como cierta o, por el contrario, si ha de rechazarse la restricción inicialmente planteada, puede establecerse de antemano el nivel de significación o trabajar con la probabilidad asociada al estadístico de prueba (p-valor). - Interpretación del resultado del contraste.
Nivel de significación y grado de confianza
Una hipótesis nula puede ser cierta o falsa y el analista puede tomar dos decisiones con respecto a ella: rechazarla o no rechazarla. Las posibilidades que existen con respecto a la hipótesis nula se resumen en la siguiente tabla:

La decisión tomada es correcta tanto si la hipótesis nula es cierta y no se rechaza —NRH_0—, como si es falsa y se rechaza —RH_0—. Si la hipótesis nula es cierta y se rechaza, se comete un error que, en estadística, se conoce como error tipo I.
- El nivel de significación \color {Black} (\alpha) es la probabilidad de cometer un error tipo I, por tanto, se define como la probabilidad de equivocarse al rechazar la hipótesis nula.
- El nivel (o grado) de confianza \color {Black} (1 \: – \: \alpha) se define como la probabilidad de no cometer un error al tomar la decisión cuando la hipótesis nula es cierta: (1 \: – \: \alpha) = 1 \: – \: P(RH_0/ H_0 \: cierta) = P(NRH_0/H_0 \:cierta)
Punto crítico
El valor crítico es un punto en la distribución de probabilidad que, bajo la hipótesis nula, sigue un estadístico de prueba y que, para un nivel de significación concreto, la divide en dos zonas: la de no rechazo y la de rechazo de la hipótesis nula. Su valor depende de los grados de libertad y del nivel de significación.
Estos valores críticos pueden obtenerse:
- Buscando su valor en las tablas de probabilidades
- Utilizando la fórmula «=INV.T.2C(Nivel de significación; grados de libertad)» que incorpora Excel
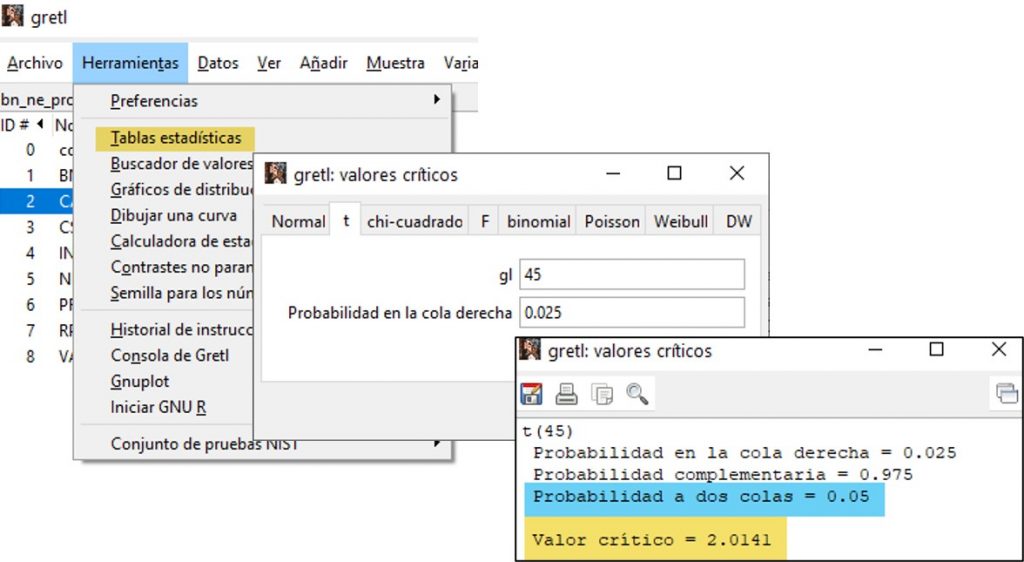
- Empleando la herramienta de Gretl «Tablas estadísticas»
Probabilidad asociada al estadístico de prueba (p-valor)
Dada una función de distribución y el valor de un estadístico de prueba en una muestra concreta, el p-valor o probabilidad asociada al estadístico de prueba es el nivel de significación a partir del cual se rechaza la hipótesis nula.
El p-valor no es único sino que depende de la función de distribución que siga el estadístico de prueba y del valor que éste tome en la muestra. Cuanto menor sea el p-valor, mayor es la evidencia para rechazar la hipótesis nula.
Cuando un contraste de hipótesis se realiza con un nivel de significación preestablecido no es necesario calcular la probabilidad asociada al estadístico de prueba, bastaría con disponer del valor del punto crítico correspondiente a la función de distribución que siga el estadístico.
Es muy habitual que los paquetes informáticos proporcionen el valor de las probabilidades asociadas junto al valor de los estadísticos de prueba en las muestras.

Este valor también puede calcularse:
- Con la fórmula que incorpora Excel, «=DISTR.T.2C(Valor absoluto(estadístico de prueba); grados de libertad)«
- Con el «Buscador de valores p» de Gretl

Grados de libertad
De forma intuitiva podría decirse que los grados de libertad son aquellos valores que dentro de un conjunto de datos, pueden escogerse libremente. Por ejemplo, al elegir 10 valores al azar tenemos completa libertad de elección. Sin embargo, si tenemos que seleccionar 10 valores cuya media aritmética es 5, solo podremos escoger libremente los nueve primeros. En efecto, en este caso hemos de elegir 10 valores cuya suma sea 50 ( \sum y = \overline {y} * Nº datos =5*10=50) y, una vez seleccionados los nueve primeros, el último tiene que ser la diferencia entre 50 y la suma de los nueve anteriores. Por tanto, no disponemos de 10 grados de libertad, sino de 9.
Si no se establece ninguna restricción, cada uno de estos números es libre de variar independientemente de los otros y, por tanto, los grados de libertad coinciden con el número de datos. Por cada restricción impuesta ha de restarse un grado de libertad. Así, por ejemplo, para calcular una varianza es necesario obtener previamente la media aritmética, luego sus grados de libertad son T – 1 , siendo T el número total de datos disponibles.
En general, puede decirse que para calcular los grados de libertad hemos de restarle al número total de datos disponibles (T) el número de restricciones impuestas.
En el caso de la suma de los cuadrados de los errores de la estimación MCO (SCE) los grados de libertad son T – (k+1) porque para calcular los errores (e_t = y_t – \widehat {y}_t = y_t -(b_0 + b_1 x_{1t} + ··· + b_k x_{kt})) han de estimarse k +1 parámetros.
Regla de decisión
Si el contraste se realiza con un nivel de significación preestablecido, para decidir si una hipótesis nula se rechaza o no, ha de comparase el valor absoluto del estadístico de prueba en la muestra con el punto crítico correspondiente.
Si |{valor \thinspace estadístico \thinspace prueba}| > valor \thinspace crítico \rightarrow RH_0
Si |{valor \thinspace estadístico \thinspace prueba}| < valor \thinspace crítico \rightarrow NRH_0
Cuando el contraste se realiza sin un nivel de significación prefijado, ha de calcularse la probabilidad asociada al estadístico de prueba (p-valor). Generalizando, la hipótesis nula se rechaza cuando esta probabilidad es inferior a los niveles de significación con los que habitualmente se trabaja (1%, 5% o 10%).
Interpretación de los resultados
Cuando la hipótesis nula se rechaza se puede afirmar que es falsa con una probabilidad de cometer un error que es igual al nivel de significación prefijado o, como mínimo, a la probabilidad asociada al estadístico de prueba.
Sin embargo, cuando no se rechaza la hipótesis nula no puede afirmarse que es correcta, sino únicamente que es compatible con los datos disponibles o dicho de otra manera, solamente puede decirse que la evidencia muestral no la contradice.