Forma funcional

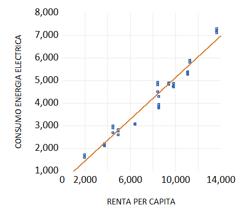Se supone, en primer lugar, que la función matemática que relaciona a la variable explicada con las explicativas, es correcta. Este supuesto es cierto siempre y cuando la función de regresión estimada coincida con la poblacional. En las aplicaciones empíricas, habitualmente, y a fin de evitar, en la medida de lo posible, un error de este tipo, se comienza representando gráficamente los datos, para determinar, de forma visual, cuál es la función matemática que mejor se adapta a la nube de puntos. 

Si esta función no es lineal —por ejemplo, si es inversa, potencial o exponencial— se convierte en lineal haciendo las transformaciones de las variables que sean necesarias. Si la no linealidad se refiere a los coeficientes \beta el método de mínimos cuadrados ordinarios no debe aplicarse.

 Selección de regresores

Se asume que los regresores que figuran en la ecuación del modelo se han seleccionado correctamente, es decir, que no se ha omitido ninguna variable relevante, ni se ha incluido ninguna irrelevante. La especificación del modelo debe basarse en la teoría económica que lo sustenta así como en el conocimiento experto de la realidad que se pretende modelizar; aún así, es práctica habitual plantear especificaciones alternativas entre las que se selecciona la más apropiada.

Datos

Se considera que no hay errores de observación en los datos. Los errores de medición pueden ser de diferente naturaleza. Entre los más frecuentes están aquellos que proceden de una selección inadecuada de la muestra o de respuestas incorrectas por parte de los encuestados y los que se derivan de errores tipográficos en la base de datos que se ha utilizado como fuente.

La importancia de utilizar adecuadamente los datos es algo obvio, sobre todo si se tiene en cuenta la posibilidad de que distintas fuentes no definan de la misma forma a las variables consideradas o incorporen cambios metodológicos, en cuyo es necesario un proceso previo de homogeneización de las series.

La perturbación aleatoria es una variable estocástica, de valores desconocidos, que recoge el efecto conjunto de todos aquellos factores que no figuran explícitamente en la ecuación del modelo. Si el modelo está correctamente especificado, estos factores, individualmente considerados, no son relevantes en la explicación del comportamiento del regresando pero, al actuar conjuntamente, ocasionan que los valores que toma la variable explicada ( Y ) se desvíen de sus valores esperados ( E(Y) = X \beta) .

Aunque insignificante, algunos de estos factores tienen un efecto positivo sobre el comportamiento del regresando mientras que en otros casos, la influencia es negativa de tal forma que, presumiblemente, se compensan. En lenguaje matemático esto equivale a decir que la esperanza matemática de la perturbación es nula:

E(\varepsilon_{t})  =0 \quad \forall t

Si este supuesto se asume, la función de regresión poblacional es:

E(Y_{t})  = \beta_{0} + \beta_{1} x_{1t} + ··· + \beta_{k} x_{kt} 

Se supone además, que las perturbaciones tienen varianzas constantes e iguales entre si (hipótesis de homocedasticidad). Es decir, se presume que estas varianzas no dependen de los valores que tomen los regresores del modelo.  En lenguaje matemático:

V(\varepsilon_{t}) = E(\varepsilon_{t} – E(\varepsilon_{t}))^2 = E(\varepsilon_{t}^{2})  =\sigma^{2} \quad \forall t

Lo que equivale a suponer que las varianzas de los elementos del vector Y son constantes e iguales entre si. Dado que:

\varepsilon_{t} = y_{t} – E(y_{t}) \rightarrow V(y_{t}) =E(y_{t} – E(y_{t}))^{2} =E(\varepsilon_{t}^{2})

Para ilustrar este concepto, planteamos el caso de un modelo uniecuacional simple en el que el comportamiento del gasto en consumo (Y) se explica en función de los ingresos semanales disponibles (X). 

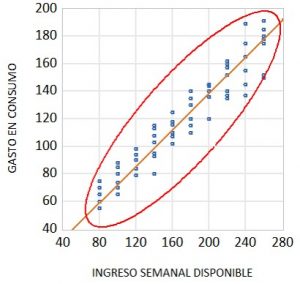La hipótesis de homocedasticidad implica admitir que la dispersión de los gastos en consumo (Y) no aumenta a medida que se incrementan los ingresos semanales disponibles (X).  Gráficamente esto se traduce en que, en este caso, la dispersión del gasto en consumo (Y) alrededor de la recta de regresión no aumenta con el nivel de ingresos semanales disponibles (X).

Esto no es lo que sucede habitualmente en la práctica ya que es lógico pensar que, mientras que los individuos de ingresos bajos raramente van a tener gastos de consumo que se desvíen de forma importante de la media de su grupo (lo impide su restricción presupuestaria); los que tienen ingresos altos tienen más posibilidades de decidir a qué dedican sus ingresos semanales y es probable que puedan registrarse diferencias importantes entre el gasto en consumo y el gasto medio.

Lo que hemos señalado permite esperar que la dispersión del gasto y, por tanto, la dispersión de la perturbación, sea más alta en el grupo de individuos que tienen ingresos elevados. Si este fuese el caso, la perturbación aleatoria sería heterocedástica y, por tanto, no tendría una varianza constante.

El incumplimiento de la hipótesis de homocedasticidad es más frecuente en modelos atemporales, en los que se consideran observaciones para distintas unidades económicas en el mismo momento del tiempo, que en modelos temporales, en los que se consideran observaciones para una unidad económica en distintos momentos del tiempo.

También se admite que las covarianzas entre perturbaciones correspondientes a diferentes observaciones son nulas (hipótesis de incorrelación), o lo que es lo mismo, se presume que no hay relaciones lineales entre ellas.

Cov(\varepsilon_{t}, \varepsilon_{s}) = E(\varepsilon_{t} – E(\varepsilon_{t}))(\varepsilon_{s} – E(\varepsilon_{s})) =E(\varepsilon_{t} · \varepsilon_{s})  =\sigma_{t,s} = 0 \quad \forall t \neq s

Lo que equivale a suponer que las covarianzas entre distintos elementos del vector Y son nulas. Dado que:

\varepsilon_{t} = y_{t} – E(y_{t}) \rightarrow Cov(y_{t}, y_{s}) =E[(y_{t} – E(y_{t}))(y_{s} – E(y_{s}))] =E(\varepsilon_{t} · \varepsilon_{s}) = 0 \quad \forall t \neq s  

Continuando con el caso del modelo que explica el comportamiento de los gastos en consumo (Y) en función de los ingresos semanales disponibles(X), esto significaría que un hecho extraordinario, como por ejemplo la visita que recibe un individuo, no afecta al gasto en consumo de otro. El incumplimiento de esta hipótesis es más frecuente en las series de tiempo que en las de corte transversal.

Finalmente, se supone que la distribución de las perturbaciones es normal. 

\varepsilon_{t} \sim N(0, \sigma^{2}) \quad \forall {t}

Esta suposición se basa en el Teorema Central del Límite que, en condiciones muy generales, garantiza que la suma de variables aleatorias, a medida que el número de sumandos aumenta, converge en distribución a una normal. 

La perturbación aleatoria recoge el efecto conjunto de todos los factores omitidos de la ecuación del modelo y, en este sentido, puede decirse que cada perturbación, formada por la «suma de infinitas variables aleatorias», sigue una distribución normal. 

En base a esta suposición se pueden deducir las distribuciones de probabilidad de los estimadores mínimo cuadráticos ordinarios (EMCO) con las que se definen los estadísticos adecuados para la inferencia estadística. 

Forma matricial

• • La esperanza matemática del vector de perturbaciones es un vector de ceros:

E( \varepsilon) = \begin{pmatrix} E( \varepsilon_{1} ) \\ E (\varepsilon_{2})  \\ ··· \\ E (\varepsilon_{T} ) \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ ··· \\ 0 \end{pmatrix}

Si este supuesto se asume, la función de regresión poblacional es:  E(Y) = X \beta

• • Para expresar en forma matricial los supuestos de incorrelación y de homocedasticidad se define la matriz de varianzas – covarianzas del vector de perturbaciones (cuyos elementos no diagonales son las covarianzas y los de la diagonal principal, las varianzas).

V( \varepsilon) = \begin{pmatrix} \sigma^{2} & 0 & ··· & 0 \\ 0 & \sigma^{2} & ··· & 0  \\ ···& ··· & ··· & ··· \\ 0 & 0 & ··· & \sigma^{2} \end{pmatrix}=  \sigma^{2} I_{T}

Esta matriz es cuadrada de orden T, simétrica —porque las covarianzas entre variables no se alteran, aunque cambie el orden en el que se disponen las mismas—, diagonal —por el supuesto de incorrelación, que establece que los elementos no diagonales son nulos— y escalar —por los supuestos de incorrelación y homocedasticidad, que establece que los elementos diagonales son iguales entre sí—.

La matriz de varianzas-covarianzas del vector Y coincide con la del vector \varepsilon: V(Y) = V(\varepsilon)= \sigma^2 I_{T}

• • La distribución del vector de perturbaciones es normal

\varepsilon \sim N(0, \sigma^{2} I_{T})

En el modelo clásico se supone que los regresores del modelo son no estocásticos, son fijos en el muestreo. Esto significa que al repetir la muestra se fijan los valores de los regresores y, aleatoriamente, se recogen los correspondientes al regresando.

Veamos un ejemplo. Partimos de los datos correspondientes a una POBLACIÓN «ficticia» formada por 60 individuos a los que se les ha preguntado por su gasto en consumo (Y) y sus ingresos semanales disponibles (X).

Elegimos  una muestra formada, por ejemplo, por 10 individuos, uno por cada nivel de ingresos.

Según esta suposición, para cambiar la muestra fijamos los valores de X y para cada uno de ellos seleccionamos, al azar, uno de los valores de Y.

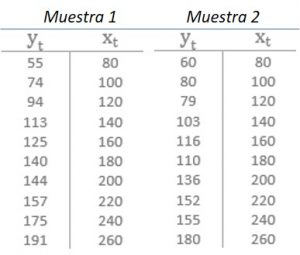
Este supuesto es bastante irreal porque si los datos se extraen mediante muestreo aleatorio simple de una única población, se elige al azar a un individuo y se recogen las cantidades correspondientes a su gasto en consumo y a sus ingresos. En este caso, las variables x e y son aleatorias, independientes e idénticamente distribuidas. 

Se admite, también, que entre los regresores no existen relaciones lineales exactas.  Si entre dos regresores existiese una relación lineal exacta (situación que se conoce con el nombre de multicolinealidad perfecta) no sería posible emplear el método de mínimos cuadrados ordinarios para estimar los parámetros del modelo porque el sistema de las T (número total de datos disponibles) ecuaciones que forman el modelo es incompatible (no tiene solución). Esta situación es muy poco frecuente en las aplicaciones empíricas en tanto en cuanto, desde un punto de vista lógico, carece de sentido incorporar a un modelo dos variables que suministran la misma información para explicar el comportamiento del regresando.

Finalmente, se supone que el número de observaciones (T) es mayor que el número de coeficientes a estimar (k +1).

Forma matricial

Todos estos supuestos hacen referencia a la matriz de regresores (X), que se supone no aleatoria.  

X = \begin{pmatrix} 1 & x_{11} & ··· & x_{k1} \\ 1 & x_{12} & ··· & x_{k2}  \\ ··· & ··· & ··· & ··· \\ 1 & x_{1T} & ··· & x_{kT} \end{pmatrix}

Esta matriz tiene T filas y (k+1) columnas y, en base a las hipótesis establecidas, el número de filas ha de ser mayor que el número de columnas. Su rango (orden de la mayor submatriz cuadrada cuyo determinante no sea nulo) puede ser, como máximo, igual a (k+1), lo que significaría que tiene (k+1) filas (o columnas) linealmente independientes, situación que se da siempre y cuando no exista multicolinealidad perfecta.  

En lenguaje matemático, esto equivale a afirmar que el rango de la matriz X es pleno (Rg X = k+1 < T).

Un modelo econométrico tiene tantos coeficientes (o parámetros) \beta como regresores. Sus valores son desconocidos y tratamos de aproximarlos a través de proceso de estimación. 

En el modelo clásico se parte del supuesto de que estos coeficientes son constantes a lo largo de la muestra o, dicho de otra manera, se asume que la estructura del modelo es única y válida para todas las observaciones muestrales. No se contempla la posibilidad de que en la relación existente entre el regresando y los regresores haya algún cambio en la muestra.

Se presume, por tanto, que los valores de los coeficientes \beta_{i} ( \forall i= 0,1, ···, k) no varían de una observación a otra.

y_1 = \beta_0 + \beta_1 x_{11} + … + \beta_k x_{k1} + \varepsilon_{1}

y_2 = \beta_0 + \beta_1 x_{12} + … + \beta_k x_{k2} + \varepsilon_{2}

································

y_T = \beta_0 + \beta_1 x_{1T} + … + \beta_k x_{kT} + \varepsilon_{T}

Forma matricial

En el modelo clásico, se asume que los elementos del vector \beta son constantes a lo largo del período muestral.

\beta = \begin{pmatrix} \beta_{0} \\ \beta_{1}  \\ ··· \\ \beta_{k} \end{pmatrix}