Contrastes de restricciones en un sólo parámetro \beta
Formulación de hipótesis
Los contrastes de hipótesis para un solo parámetro, pueden ser de dos tipos:
- Bilateral
La hipótesis nula es que el parámetro toma un valor concreto —al que denominaremos \beta_i^* — y la alternativa es que pueda tomar cualquier otro diferente al que se le asigna en la hipótesis nula:
H_0: \beta_i = \beta_i^*
H_1: \beta_i \neq \beta_i^*
Si el valor que se establece en la hipótesis nula es el cero, se dice, entonces, que la restricción es de nulidad. Este contraste se conoce con el nombre de contraste de relevancia individual de las variables explicativas del modelo porque si el valor del parámetro \beta_i fuese cero eso significaría que —manteniéndose constante las restantes variables explicativas consideradas— las variaciones de la variable x_i no provocan cambios en el regresando, o dicho de otra manera, la variable x_i no es determinante para explicar el comportamiento del regresando.
H_0: \beta_i = 0
H_1: \beta_i \neq 0
- Unilateral
La hipótesis nula es que el parámetro toma un valor valor concreto y la alternativa que es mayor o menor al asignado en la hipótesis nula.
El contraste es de cola derecha si la hipótesis alternativa es que el valor del parámetro es mayor que el que se le asigna en la hipótesis nula.
H_0: \beta_i = \beta_i^*
H_1: \beta_i > \beta_i^*
Si la hipótesis alternativa es que el valor del parámetro es menor que el que se le asigna en la hipótesis nula, es un contraste de cola izquierda.
H_0: \beta_i = \beta_i^*
H_1: \beta_i < \beta_i^*
Estadístico de prueba
\Large t_i = \frac{b_i – \beta_i^*}{S_{b_i}} \sim t_{T – k- 1 }
Para realizar el contraste es necesario calcular el valor del estadístico en la muestra.
Regla de decisión
Si el contraste se realiza con un nivel de significación preestablecido, ha de compararse el valor del estadístico de prueba en la muestra con el punto crítico correspondiente a una t-Student con T – k – 1 grados de libertad (tabla ).
- Contraste bilateral
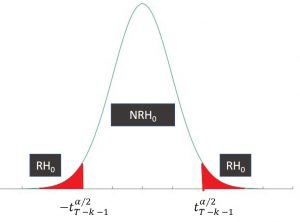
Si |t_i| > t^{\alpha/2}_{T – k -1} \rightarrow RH_0
Si |t_i| < t^{\alpha/2}_{T – k -1} \rightarrow NRH_0
- Contraste unilateral cola derecha

Si t_i > t^{\alpha}_{T – k -1} \rightarrow RH_0
Si t_i < t^{\alpha}_{T – k -1} \rightarrow NRH_0
- Contraste unilateral cola izquierda
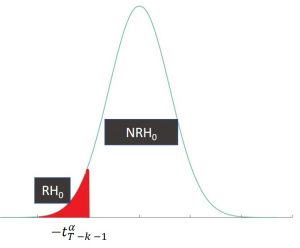
Si t_i < – t^{\alpha}_{T – k -1} \rightarrow RH_0
Si t_i > – t^{\alpha}_{T – k -1} \rightarrow NRH_0
Si el contraste se realiza sin un nivel de significación preestablecido, ha de valorarse si la probabilidad mínima de equivocarse al rechazar la hipótesis nula —probabilidad asociada al estadístico de prueba o p-valor— es grande o pequeña. Habitualmente, si la probabilidad asociada al estadístico de prueba es mayor que los niveles de significación con los que se suele trabajar —1%, 5% o 10%— no se rechaza la hipótesis nula.
En las salidas de la estimación que proporcionan todos los programas especializados, figuran los valores de estos estadísticos en la muestra junto con sus probabilidades asociadas.
Ha de tenerse en cuenta que la probabilidad asociada a un estadístico de prueba nunca va a ser exactamente igual a cero —probabilidad que corresponde a un suceso imposible— lo que puede suceder es que las celdas en las que aparecen estas probabilidades estén formateadas para cuatro o seis decimales y, cuando la evidencia en contra de la hipótesis nula es muy fuerte, su valor es muy pequeño. En estos casos, la hipótesis nula se rechaza prácticamente a cualquier nivel de significación.
Caso práctico: modelo del beneficio de las empresas
BN_t = \beta_0 + \beta_ 1 NE_t + \beta_2 PRO_t + \beta_3 RP_t + \beta_4 CS_t + \varepsilon_t

Para responder a las preguntas de si realmente el ‘Número de empleados’ puede considerarse un factor determinante de los beneficios o si podría asumirse que —manteniéndose constante las restantes variables explicativas del modelo— por cada unidad producida el beneficio de las empresas aumentaría en 200 euros, ha de realizarse un contraste bilateral de un sólo parámetro.
Se realizaría un contraste unilateral si, por ejemplo, se planteasen cuestiones tales como si la relación existente entre la ‘Producción’ y el ‘Beneficio’ es directa o si los ‘Costes Salariales’ tienen un efecto negativo sobre los beneficios.
Contraste de relevancia individual de los regresores del modelo
El parámetro \beta_1 sería cero si —manteniéndose constantes las demás variables explicativas del modelo— los beneficios no variasen al modificarse el número de empleados. Se trata, por tanto, de un contraste bilateral de restricciones cero; es decir, un contraste de relevancia individual de la variable explicativa ‘Número de empleados‘.
Hipótesis nula y alternativa:
H_0: \beta_1 = 0
H_1: \beta_1 \neq 0
Estadístico de prueba:
t_1 = \frac{b_1}{S_{b_1}} \sim t_{45}
Valor del estadístico en la muestra:
t_1 = \frac{6,2147E-05}{4,9766E-05} = 1,249
Regla de decisión e interpretación:
En la columna «Estadístico t» de la salida de la estimación MCO, figuran los valores en la muestra de los estadísticos de prueba para realizar el contraste de relevancia individual de los regresores del modelo y en la columna «valor p» las probabilidades asociadas a estos estadísticos.
- Prob(t_0) = 0,0030 < 0,01 permite concluir que el modelo ha de incorporar regresor ficticio.
- Prob(t_1) = 0,2182 indica que la hipótesis nula ( H_0: \beta_1 = 0 ) se rechaza a niveles de significación superiores al 21,82%.
En este caso, la probabilidad de cometer un error al rechazar la hipótesis nula es muy elevada y, a los niveles de significación habituales —1%, 5% o 10%— , no se rechaza la hipótesis nula ya que el valor p es mayor que cualquiera de estos niveles de significación. Por tanto, para estos niveles de significación, la variable ‘Número de Empleados’ no se muestra individualmente relevante.
No rechazar una hipótesis nula no significa que la hipótesis sea cierta, sino que la evidencia muestral es compatible con la hipótesis inicialmente planteada.
Las variables ‘Producción’ y ‘Recursos Propios‘ son individualmente relevantes prácticamente a cualquier nivel de significación porque las probabilidades asociadas a los correspondientes estadísticos de prueba son muy pequeñas (cualquiera de ellas es inferior a 0,01).
- Prob(t_2) = 1,75E-010
- Prob(t_3) = 4,53E-05
En el caso de la variable ‘Costes Salariales’ :
- Prob(t_4) = 0,0255 indica que la hipótesis nula H_0: \beta_4 = 0 se rechaza a niveles de significación superiores al 2,55%.
Al nivel de significación del 5% sí se rechaza la hipótesis nula porque Prob(t_4) = 0,0255 < 0,05 y, a este nivel de significación, esta variable es individualmente relevante. Sin embargo, al nivel de significación del 1%, esta variable no se muestra individualmente relevante.
- Prob(t_4) = 0,0255 indica que la hipótesis nula H_0: \beta_4 = 0 se rechaza a niveles de significación superiores al 2,55%.
Otros contrastes bilaterales
Para responder a la pregunta de si podría asumirse que —manteniéndose constantes las restantes variables explicativas del modelo— por cada unidad producida, el beneficio de las empresas aumentaría en 200 euros (0,2 miles de euros), ha de realizarse un contraste bilateral de un sólo parámetro:
H_0: \beta_2 = 0,2
H_1: \beta_2 \neq 0,2
Estadístico de prueba:
t_2 = \frac{b_2 -\beta_2^*}{S_{b_2}} \sim t_{45}
Valor del estadístico en la muestra:
t_2 = \frac{0,101933 – 0,2}{0,0124255} = -7,8924
Regla de decisión e interpretación:
- Para un nivel de significación preestablecido del 5%:
En este caso, ha de compararse el valor absoluto del estadístico de prueba en la muestra con el punto crítico correspondiente a una distribución t-Student con 45 (T – k – 1 =50 – 4 – 1) grados de libertad.
- Para un nivel de significación preestablecido del 5%:
|t_2| =7,89 > t^{\alpha/2}_{T – k -1} =2,0141 \rightarrow RH_0
Al nivel de significación del 5%, no puede asumirse que —manteniéndose constante las restantes variables explicativas del modelo— por cada unidad producida, por término medio el beneficio de las empresas aumente 200 euros (0,2 miles de euros).
- Si no se preestablece el nivel de significación, ha de calcularse la probabilidad asociada al estadístico de prueba (p-valor).
En este caso, la probabilidad asociada al estadístico de prueba es muy pequeña (Prob(t_2) = 4,9459E-010) por lo que puede concluirse que la hipótesis nula H_0: \beta_2 = 0,2 se rechaza prácticamente a cualquier nivel de significación.
Si lo que se desea es conocer el rango de valores de un parámetro que son compatibles con la información muestral disponible, ha de calcularse el intervalo de confianza correspondiente.
Contrastes unilaterales
Para responder a cuestiones como si la relación existente entre la producción y el beneficio es directa o si los costes salariales tienen un efecto negativo sobre los beneficios ha de recurrirse a contrastes unilaterales.
Contraste cola derecha
En el primer caso, si la relación existente entre la producción y los beneficios fuese directa, el parámetro \beta_2 tomaría valores positivos. Las hipótesis que han de plantearse son:
H_0: \beta_2 = 0
H_1: \beta_2> 0
El estadístico de prueba (t_2 = b_2 /S_{b_2} ) sigue una distribución t-Student con 45 (T-k-1 = 50-4-1) grados de libertad.
Regla de decisión e interpretación:
- Si el contraste se realiza con un nivel de significación preestablecido, ha de compararse el valor del estadístico en la muestra con el punto crítico.
t_2 =8,204 > t^{\alpha}_{T – k -1} =1,679 \rightarrow RH_0
Al nivel de significación del 5%, puede afirmarse que entre los beneficios y la producción existe una relación de tipo directo.
- Si no se preestablece el nivel de significación, ha de calcularse la probabilidad asociada al estadístico de prueba (p-valor) porque el que figura en la salida de la estimación mínimo cuadrática ordinaria corresponde a un contraste bilateral de restricciones cero.
Prob (t_2) = 8,71632E-011
La hipótesis nula se rechaza prácticamente a cualquier nivel de significación.
Contraste cola izquierda
Para responder a la pregunta de si los costes salariales tienen un efecto negativo sobre los beneficios hacemos un contraste unilateral de cola izquierda.
H_0: \beta_4 = 0
H_1: \beta_4 < 0
Regla de decisión e interpretación:
- El valor del estadístico de prueba en la muestra es -2,311 y el del del punto crítico, al nivel de significación del 5%, es -1,679.
t_4 = -2,311 < – t^{\alpha}_{T – k -1} = -1,679 \rightarrow RH_0
Al nivel de significación preestablecido, la hipótesis de que los costes salariales tienen un efecto negativo sobre los beneficios es asumible en base a la información muestral disponible.
- La probabilidad asociada al estadístico de prueba (0,0127354) indica que la hipótesis alternativa es asumible para niveles de significación superiores al 1,27%.
Intervalos de confianza para los parámetros \beta_i
Cuando son asumibles varias hipótesis diferentes sobre el valor de un parámetro, puede resultar útil construir su intervalo de confianza a fin de conocer qué rango de valores son compatibles con la evidencia muestral.
Construir un intervalo de confianza consiste en obtener los extremos de un intervalo que, con una probabilidad elevada, contiene al parámetro. O dicho de otra manera, este intervalo contiene el verdadero valor del parámetro en el (1-\alpha) \times 100 de todos los intervalos que se construyan para todas las posibles muestras del mismo tamaño que podrían ser seleccionadas.
Para calcular sus extremos, ha de fijarse de antemano el nivel de confianza [( 1 -\alpha) \times 100] que suele ser del 90%, del 95% o del 99%. Ha de tenerse en cuenta que cuanto mayor es el nivel de confianza, más amplio resulta el intervalo y más imprecisa será la información que proporcione.
Los extremos del intervalo de confianza para un parámetro \beta_i se obtienen a través de la expresión:
(b_i – S_{b_i} t^{\alpha/2}_{T-k-1}; b_i + S_{b_i} t^{\alpha/2}_{T-k-1})
y proporciona el conjunto de valores de \beta_i que no podrían ser rechazados en un contraste bilateral al nivel de significación del (\alpha \times 100)%, es decir, el conjunto de valores del parámetro que son compatibles con la información muestral disponible.
Si el intervalo de confianza contiene valores de un parámetro muy próximos a uno concreto, la evidencia empírica indica que su valor real no está alejado de dicha magnitud. Si, por el contrario, contiene valores alejados de uno concreto, el intervalo de confianza proporciona un conocimiento impreciso del verdadero valor del parámetro.
Cálculo e interpretación
Intervalo de confianza del 90% para el parámetro \beta_2 es:
(0,101933 – 1,679 \times 0,0124255 ; 0,101933 + 1,679 \times 0,0124255) = (0,0810651; 0,122800)
Interpretación:
- Al nivel de significación del 10%, puede afirmarse que la variable ‘Producción‘ es individualmente relevante —el cero no está dentro del intervalo— y que tiene un efecto positivo sobre los beneficios —no hay ningún valor negativo compatible con la información muestral—.
- También podría afirmarse que —manteniéndose constante las restantes variables explicativas consideradas— no es posible que por cada unidad producida, los beneficios aumenten en 200 euros, puesto que el valor 0,2 esta fuera del intervalo de confianza y, por tanto, la hipótesis nula H_0: \beta_2 =0,2 se rechazaría.
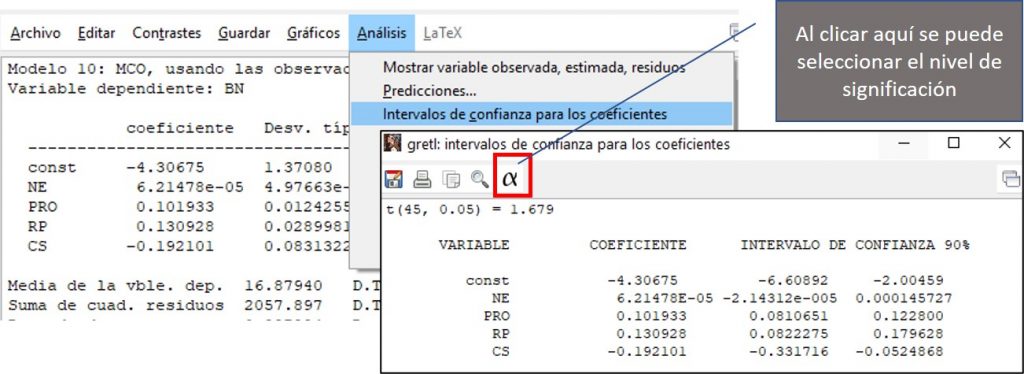
Los intervalos de confianza pueden obtenerse con Gretl, seleccionando la opción «Intervalos de confianza para los coeficientes» del grupo «Análisis» en la pantalla en la que se presentan los resultados de la estimación.