Contraste de nulidad conjunta de los coeficientes angulares del modelo
Permite analizar si el efecto conjunto de las variables explicativas en la explicada es estadísticamente significativo, es decir, si dichas variables son conjuntamente relevantes para explicar el comportamiento del regresando (contraste de relevancia conjunta).
H_0: \beta_1 = \beta_2 = \beta_3 =\beta_4 = 0
H_1: alguno \thinspace \neq 0
Tan solo tiene sentido realizar este contraste cuando ninguna de las variables explicativas se muestran individualmente relevantes, situación que puede presentarse cuando en el modelo existe un elevado grado de multicolinealidad.
Caso práctico: modelo del beneficio de las empresas
Estadístico de prueba
El estadístico de prueba, bajo la hipótesis nula, sigue una distribución F de Snedecor:
F = \frac{R^2/k}{(1 – R^2)/(T-k-1)} \sim F_{(k,T-k-1)}
donde R^2 es el coeficiente de determinación del modelo, k el número de variables explicativas y T el número observaciones con las que se ha efectuado la estimación.
Regla de decisión
Si el valor del estadístico en la muestra es superior al punto crítico, F^{\alpha}_{(k,T-k-1)} , la hipótesis nula se rechaza. 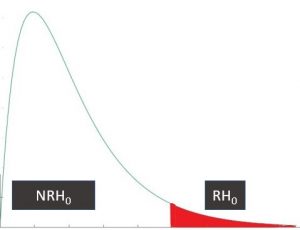
F = 869,286 > F^{0,05}_{4,45} = 2,579 \rightarrow RH_0
Si no se preestablece el nivel de significación, el contraste se realiza con la probabilidad asociada al estadístico de prueba que figura en la salida de la estimación MCO. En este ejemplo, el valor p es tan pequeño que, prácticamente a cualquier nivel de significación, se rechaza la hipótesis nula.
Contrastes para restricciones lineales en los parámetros
En ocasiones se plantean hipótesis conjuntas sobre los parámetros del modelo. Por ejemplo, si las variables ‘Número de Empleados‘ y ‘Coste Salarial‘ son conjuntamente relevantes o si podría admitirse que los ‘Recursos Propios’ y los ‘Costes Salariales’ tienen el mismo efecto sobre los beneficios, pero de sentido contrario.
En general, cuando se establecen restricciones lineales exactas respecto a los parámetros, el contraste se realiza a través de un estadístico (Test de Wald) que se basa en el cálculo de las sumas de cuadrados de errores de dos regresiones. En la primera, que se denomina regresión con restricciones o restringida, se impone el cumplimiento de la hipótesis nula y en la segunda, conocida como regresión sin restricciones, no.
Este método no suele emplearse cuando se utiliza un procedimiento que no requiere la estimación del modelo con restricciones (como, por ejemplo, en el caso de contrastes de relevancia individual o conjunta de las variables explicativas del modelo) y no es válido para realizar contrastes de restricciones de desigualdad, lineales pero estocásticas, no lineales, etcétera.
Estadístico de prueba
Este estadístico de prueba – conocido como test de Wald – que bajo la hipótesis nula sigue una distribución F de Snedecor, se basa en la comparación de dos sumas de cuadrados de errores: la del modelo con restricciones – SCE_R – en el que se supone cierta la hipótesis nula, y la del modelo sin restricciones – SCE – en el que la hipótesis que se supone cierta es la alternativa.
F = \frac{(SCE_R – SCE)/(k – k_R)}{SCE/ (T – k – 1)}\sim F_{(k-k_R, T-k-1)}
Mínimos cuadrados con restricciones
Para obtener el valor del estadístico de prueba en la muestra es necesario estimar el modelo con restricciones. Esta estimación se efectúa por mínimos cuadrados ordinarios una vez sustituida la restricción que se establece en la hipótesis nula en la ecuación del modelo sin restricciones.
Regla de decisión
Este valor del estadístico en la muestra se compara con el punto crítico correspondiente.
F > F^{\alpha}_{(k – k_R, T – k -1)} \rightarrow RH_0
F < F^{\alpha}_{(k – k_R, T – k -1)} \rightarrow NRH_0
o bien se calcula la probabilidad asociada al valor que toma el estadístico de prueba en la muestra.
Caso práctico: modelo del beneficio de las empresas
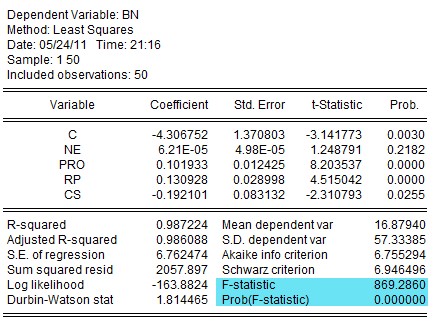
El modelo sin restricciones
BN_t = \beta_0 + \beta_1 NE_t + \beta_2 PRO_t + \beta_3 RP_t + \beta_4 CS_t + \varepsilon_t
se ha estimado por mínimos cuadrados ordinarios. El valor obtenido para la suma de cuadrados de errores es SCE = 2057, 897 y k —número de variables explicativas— es 4.
Contraste de nulidad de un subconjunto de parámetros
¿Son conjuntamente relevantes las variables ‘Número de Empleados‘ y ‘Coste Salarial‘?
H_0: \beta_1 = \beta_4 = 0
H_1: alguno \neq 0
Al nivel de significación del 5%, la variable ‘Coste Salarial‘ es individualmente relevante y, por tanto, la hipótesis nula se rechaza.
Sin embargo, al nivel de significación del 1%, ninguna se muestra individualmente relevante y, en este caso, vamos a comprobar si la hipótesis de que ambos parámetros son simultáneamente nulos, es compatible con la información muestral disponible.
Modelo con restricciones:
Si la hipótesis nula fuese cierta, la ecuación del modelo sería:
BN_t = \beta_0 + \color {red} {0} \color {black} · NE_t + \beta_2 PRO_t + \beta_3 RP_t + \color {red} {0} \color {black} · CS_t + \varepsilon_t
BN_t = \beta_0 + \beta_2 PRO_t + \beta_3 RP_t + \varepsilon_t
Este modelo se estima por mínimos cuadrados ordinarios, para obtener el valor de la suma de cuadrados de errores del modelo restringido (SCE_R).

Cálculo del estadístico:
El estadístico de prueba sigue una distribución F de Snedecor con 2 (k – k_R ) grados de libertad en el numerador y 45 (T – k – 1) en el denominador . Su valor en la muestra es:
F = \frac{(2382,164 – 2057,897)/(4-2)}{2057,897/(50-4-1)} = 3,5454
Regla de decisión e interpretación:
F = 3,5454 < F^{0,01}_{(2,45)} = 5,11032 \rightarrow NRH_{0}
Al nivel de significación del 1%, es asumible que las variables ‘Numero de Empleados‘ y ‘Coste Salarial‘ no se muestran conjuntamente relevantes.
Contraste de una combinación lineal de parámetros
¿Puede admitirse que las variables ‘Recursos Propios’ y ‘Costes Salariales‘ tienen el mismo efecto sobre los beneficios pero de sentido contrario?
H_0: \beta_3 = – \beta_4
H_1: \beta_3 \neq – \beta_4
Modelo con restricciones:
Para obtener la ecuación del modelo con restricciones se sustituye la restricción establecida en la hipótesis nula en la ecuación del modelo sin restricciones:
BN_t = \beta_0 + \beta_1 NE_t + \beta_2 PRO_t + \beta_3 RP_t \thinspace + \thinspace \color {red} {\beta_4} \color {black} CS_t + \varepsilon_t
BN_t = \beta_0 + \beta_1 NE_t + \beta_2 PRO_t + \beta_3 RP_t \thinspace – \thinspace \color {red} {\beta_3} \color {black} CS_t + \varepsilon_t
BN_t = \beta_0 + \beta_1 NE_t + \beta_2 PRO_t + \color {red} \beta_3 (RP_t \thinspace – \thinspace CS_t ) \color {black}+ \varepsilon_t
A continuación se estima el modelo que relaciona al beneficio con las restantes explicativas que figuran en la ecuación con restricciones:

Cálculo del estadístico:
En este caso, el estadístico sigue una distribución F_Snedecor con 1 (k – k_R ) grados de libertad en el numerador y 45 (T – k – 1) en el denominador cuyo valor en la muestra es:
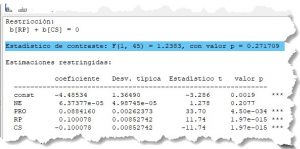
F = \frac{(2114,526- 2057,897)/(4-3)}{2057,897/(50-4-1)} = 1,2383
Regla de decisión e interpretación:
F = 1,2383 < F^{0,05}_{(1,45)} = 4,057 \rightarrow NRH_{0}
Al nivel de significación del 5% —como ambas variables están expresadas en la mismas unidades de medida— puede decirse que es asumible la hipótesis de que las variables ‘Recursos Propios‘ y ‘Coste Salarial‘ tienen el mismo efecto sobre los beneficios aunque de sentido contrario.
Test de Wald con EViews y con Gretl
Los paquetes informáticos especializados incorporan una funcionalidad que permite realizar los contrastes de restricciones lineales exactas en los parámetros de forma automática.
Tanto en Gretl como en Eviews se accede desde la cinta de opciones de la pantalla de la estimación MCO.
- Gretl : «Contrastes» – «Restricciones lineales«
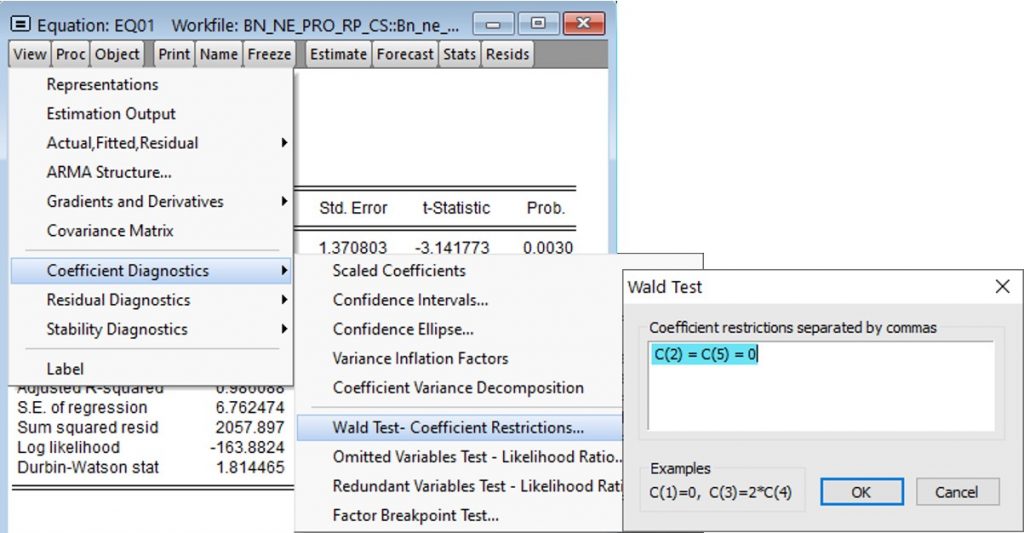
- EViews: «View«- «Coefficient Diagnostics» –«Wald Test. Coefficient Restrictions».
En ambos casos, para introducir la restricción lineal ha de utilizarse la notación que cada programa emplea. Los coeficientes se numeran por el orden que ocupan en la ecuación del modelo, comenzando por el número 1 y no por el 0.
- Gretl designa a los coeficientes con la letra «b» indicando a continuación entre corchetes el orden que ocupa en la ecuación -por ejemplo b[2] – o el nombre de la variable a la que acompañan b[NE] .
- EViews utiliza la letra «C» seguida del orden que ocupa en la ecuación escrito entre paréntesis – por ejemplo, C(2) .
Caso práctico: modelo del beneficio de las empresas
EViews
La hipótesis nula del primer contraste H_0: \beta_1 = \beta_4 =0 , traducida a la notación empleada en EViews es H_0: C(2) = C(5) =0 .
El resultado del contraste
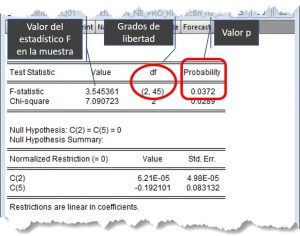
permite concluir que la hipótesis nula H_0: \beta_1 = \beta_4 =0 se rechaza para niveles de significación superiores al 3,72%.
El resultado del segundo contraste planeado H_0: \beta_3 = -\beta_4 o en notación de EViews H_0: C(4) = -C(5) permite concluir que esta hipótesis es compatible con la información muestral disponible para los niveles de significación de uso habitual (1%, 5% o 10%).

Gretl
La hipótesis nula del primer contraste H_0: \beta_1 = \beta_4 =0 , traducida a la notación empleada en Gretl es H_0: b[2] = b[5] =0 o bien H_0: b[NE] = b[CS] =0 .
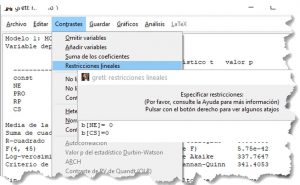
El resultado del contraste permite concluir que la hipótesis nula H_0: \beta_1 = \beta_4 =0 se rechaza para niveles de significación superiores al 3,72%.

El resultado del segundo contraste planeado H_0: \beta_3 = -\beta_4 o en notación de Gretl H_0: b[RP] + b[CS] = 0 permite concluir que esta hipótesis es compatible con la información muestral disponible para los niveles de significación de uso habitual (1%, 5% o 10%).