Análisis de la calidad del ajuste

Una vez estimado el modelo por MCO ha de valorarse en qué medida la función de regresión estimada describe los datos. 

El método de mínimos cuadrados ordinarios consiste en seleccionar aquella función de regresión estimada que minimiza la suma de los cuadrados de los errores, es decir, aquella con la que se cometen los menores errores posibles, lo que no significa que sean pequeños. En otras palabras, la función de regresión estimada es la que mejor se ajusta a la nube de puntos, pero esto no quiere decir que se ajuste bien. 

Caso práctico: modelo para el consumo de energía

Para medir el efecto de la renta per cápita (expresada en miles de euros) sobre el consumo de energía (expresado en kilovatios/hora), se han recogido datos para 50 individuos y se ha estimado por MCO el modelo que relaciona a ambas variables.

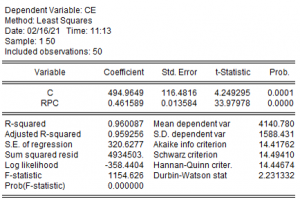
¿Podría decirse que las observaciones están muy agrupadas alrededor de la recta de regresión estimada o, por el contrario, están muy dispersas? ¿Qué parte de la variación del consumo de energía explica la regresión?¿la renta per cápita explica bien el consumo de energía?

Para responder a estas preguntas, podríamos representar gráficamente la nube de puntos y valorar, intuitivamente, si la recta de regresión estimada se ajusta bien a los datos.

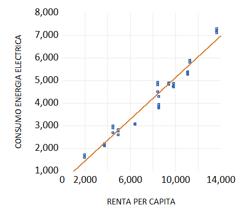
Pero, ¿estamos seguros de nuestro criterio? ¿cómo lo hacemos si el modelo es múltiple (más de una variable explicativa) teniendo en cuenta que, en este caso, la función de regresión estimada es un hiperplano?

Lo más útil es disponer de medidas que resuman esta información y nos permitan evaluar la calidad del ajuste efectuado.

Medidas evaluadoras de la calidad del ajuste

La bondad del ajuste depende de lo próximos que estén los valores observados y estimados del regresando; es decir, del tamaño de las distancias que hay desde cada uno de los puntos del diagrama de dispersión a la función de regresión estimada o, lo que es lo mismo, del tamaño de los errores de la estimación.

En definitiva, se trata de medir qué parte de la variación total del regresando en la muestra queda explicada por la regresión efectuada y qué parte no.

La variación total del regresando en la muestra es su varianza muestral:

V(y_t) = \frac {\sum _{t=1} ^T {(y_t – \overline{y})^2}}{T} = \frac {SCT}{T}

Una parte de esta variación queda explicada por la variabilidad de los valores estimados del regresando —V( \widehat {y}_t )— y la otra, debida a la dispersión de los errores de estimación — V(e_t)— no.

V(\widehat {y}_t) = \frac {\sum _{t=1} ^T {(\widehat {y}_t – \overline{\widehat {y}})^2}}{T} = \frac {SCR}{T}

Y, suponiendo un modelo con ordenada en el origen:

\sum_{t=1}^T e_{t} = \sum_{t=1}^T (y_{t} – \widehat {y}_t ) = 0

por tanto:

V(e_t) = \frac {\sum _{t=1} ^T {(e_t – \overline{e})^2}}{T} =\frac {\sum _{t=1} ^T {e_t^2}}{T} = \frac {SCE}{T}

Dado que las tres expresiones tienen denominador común (T), para valorar la calidad del ajuste se comparan las tres sumas de cuadrados: la de totales (SCT), la de la regresión (SCR) y la de errores (SCE).

En modelos con ordenada en el origen, es posible demostrar que:

SCT = SCE + SCR

la suma (de cuadrados) total se descompone en dos partes: la «suma no explicada» (SCE) y la «suma explicada» (SCR).

El ajuste es tanto mejor cuanto menor es el peso de la suma de cuadrados de errores (SCE) sobre la suma de cuadrados de totales (SCT) o cuanto más similares son los valores de la suma de cuadrados de la regresión (SCR) y la de totales (SCT). Para comparar estas magnitudes, se utiliza el coeficiente de determinación.

R^2 = 1 – \frac {SCE}{SCT} = \frac{SCR}{SCT}

El R^2 es la proporción de la varianza muestral del regresando explicada por la función de regresión mínimo cuadrática ordinaria, es decir, por las variaciones de las variables explicativas incluidas en la ecuación del modelo.

El valor de R^2:

    • no puede ser negativo ya que en los  modelos con ordenada en el origen, puede definirse como el cociente entre dos sumas de cuadrados
    • no puede ser superior a la unidad porque la «suma explicada» (SCR) no puede ser superior a la suma (de cuadrados) total.

Cuando se cumplen las propiedades del ajuste MCO, el valor mínimo del coeficiente de determinación es cero y su valor máximo uno. 

Si R^2 toma un valor bajo es recomendable revisar la especificación del modelo ya que probablemente se haya cometido un error o bien en la forma funcional o bien la selección de regresores.  

En la práctica no toma valores extremos y, en general, es indicativo de un buen ajuste si su valor es superior 0,9.

La raíz del error cuadrático medio, si el modelo tiene ordenada en el origen, es la desviación típica muestral de los errores.

RECM = \widehat \sigma = \sqrt \frac{SCE}{T}

Para analizar la bondad del ajuste, su valor se expresa en porcentaje respecto a la media muestral del regresando:

 %RECM = \frac{RECM}{\overline y} * 100

e indica cuál es, por término medio, el porcentaje de error que se comete al estimar los valores del regresando utilizando el modelo. Cuanto menor sea su valor, mejor será el ajuste. En general, se considera que esta medida es indicativa de un buen ajuste si el %RECM es inferior al 5%.

En general, se considera que el ajuste es bueno si R^2 es superior a 0,9 y %RECM inferior al 5%.

Para analizar la calidad del ajuste, es conveniente calcular tanto R^2 como %RECM porque, en algunos casos, pueden proporcionar informaciones contradictorias. 

Tanto R^2 como %RECM son medidas relativas. El coeficiente de determinación no solo depende de la «suma no explicada», sino también de la suma (de cuadrados) totales  y el porcentaje de la raíz del error cuadrático medio depende también de la media muestral del regresando.

    1. Cuando la variable explicada tiene un recorrido muy amplio, su varianza en la muestra y, por tanto la suma de cuadrados de totales, es muy elevada y, aunque SCE sea elevada el R^2 puede resultar próximo a la unidad. Sin embargo, en el cálculo del %RECM no interviene SCT y, por tanto, si SCE es elevada, tomará un valor elevado.
      En este caso, mientras que el valor de R^2 es indicativo de un buen ajuste el del %RECM indica lo contrario.
      ¿Cuál de las dos medidas resulta más fiable? Ninguna, porque aunque al %RECM no le afecta el elevado valor de la suma (de cuadrados) totales, sí depende de la media muestral del regresando que, en este caso, no es representativa de sus valores.
      ¿Cómo se valora, en este caso, la calidad del ajuste? Analizando el tamaño de los errores relativos: \lvert {eR_{t}} \lvert = \lvert{\frac {e_t}{y_t}} \lvert \times 100.  Si mayoritariamente son elevados —superiores al 5%— el ajuste es malo.
    2. Cuando la variable explicada tiene un escaso recorrido, su varianza muestral es muy pequeña y, aunque SCE sea baja, R^2 puede tomar un valor próximo a cero, mientras que %RECM será bajo porque no está afectado por SCT. Así, R^2 es indicativo de un mal ajuste y %RECM de un buen ajuste.
      En este caso, es más fiable el valor del %RECM porque la media es muy representativa de los valores de la variable explicada.
  1.  

Caso práctico: modelo consumo de energía - renta

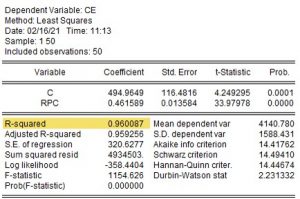
Estimación MCO del modelo Consumo Energía

El valor del coeficiente de determinación está próximo a uno, por lo que puede decirse que, según esta medida, el ajuste es bueno. El modelo explica, aproximadamente, el 96% de las variaciones muestrales del consumo de energía (R^2 \times 100 \approx 0,96% ). 

RECM = \widehat \sigma = \sqrt \frac{4934503}{50} = 314,15

 %RECM = \frac{314,15}{4140.78} \times 100 = 7,59%

Por término medio, el porcentaje de error que se comete al estimar los valores del consumo de energía utilizando este modelo es del 7,59%. Según esta medida, el ajuste no es bueno.

En este caso, no es posible evaluar la calidad del ajuste con estas medidas.

Medidas para comparar la calidad del ajuste

Los valores del coeficiente de determinación y del porcentaje de la raíz del error cuadrático medio no son válidos para comparar el ajuste de modelos alternativos (modelos referidos a la misma endógena, para la misma muestra y con distinto número de variables explicativas) porque a medida que aumenta el número de regresores, la suma de cuadrados de errores disminuye y, como SCT y la media muestral del regresando no cambian, el valor de R^2 aumenta y el del %RECM disminuye. 

La inclusión de variables explicativas adicionales ocasiona siempre una disminución de SCE y una pérdida de grados de libertad. Para comparar la calidad del ajuste ha de valorarse si la disminución en SCE se compensa, o no, con la reducción de los grados de libertad. Dicho de otra manera, ha de penalizarse la inclusión de variables explicativas irrelevantes en la explicación del comportamiento del regresando. Por esta razón, para comparar la calidad del ajuste tanto SCE como SCT se corrigen por sus correspondientes grados de libertad.

Si se ha realizado alguna transformación del regresando (por ejemplo, se han tomado logaritmos), aún cuando se haya utilizado la misma muestra, para comparar las calidades de los ajustes ha de tenerse en cuenta que los modelos se ajustan a dos variables explicadas distintas.  

El coeficiente de determinación ajustado es una modificación de R^2. Su valor no aumenta necesariamente al incluir variables explicativas adicionales.

\overline {R}^2 = 1 – \thinspace \large{\frac{SCE/(T – k – 1)}{SCT/(T -1)}} = \normalsize 1 \thinspace – \thinspace \large{\frac{T – 1}{T – k – 1}\frac{SCE}{SCT}} = \normalsize 1 \thinspace – \thinspace \large{\frac{T – 1}{T – k – 1} } (1 – R^2)

Dado que el cociente entre (T – 1) y (T – k – 1) es siempre mayor que la unidad, el valor de \overline {R}^2 siempre es menor que el de R^2.

A diferencia del coeficiente de determinación, el valor de \overline {R}^2 puede ser negativo. 

Cuando se incorpora una variable adicional a un modelo, SCE disminuye y el cociente entre (T – 1) y (T – k – 1) aumenta. Si se añade una variable explicativa relevante, la disminución de SCE no se compensa con la pérdida de grados de libertad y eso provocará un mayor \overline {R}^2 y, por tanto, un mejor ajuste.

El error estándar de la regresión es la cuasi desviación típica muestral de los errores.

ES = S = \sqrt {s^2} = \sqrt \frac{SCE}{(T – k -1)}

Para analizar la bondad del ajuste, su valor se expresa en porcentaje respecto a la media muestral del regresando:

 %ES = \frac{ES}{\overline y} \times 100

Su valor es mayor que %RECM ya que T – k – 1 < T y no siempre disminuye cuando se incorporan nuevos regresores al modelo.

Caso práctico: modelo consumo de energía - renta - precios

En la ecuación del modelo que explica el comportamiento del consumo de energía, se incorpora, como variable explicativa el precio de la energía (PE), expresada en euros por kilovatio hora.

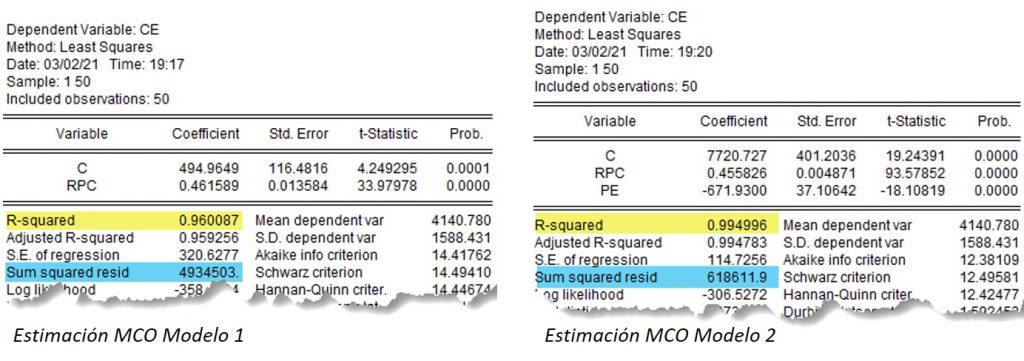
Al aumentar k —número de variables explicativas— la suma de cuadrados de errores disminuye:

\bigtriangledown {SCE} = 4.934.503 – 618.611,9 = 4.315.891,1

y se pierde un grado de libertad. Como la suma de cuadrados de totales no cambia, ya que en ambos casos se utiliza la misma muestra y la variable explicada es la misma, el valor de R^2 aumenta. Esto no quiere decir que el ajuste mejore. 

En este caso, el valor de \overline {R}^2 en el primer modelo es inferior al del segundo, por tanto es mejor la calidad del ajuste del modelo 2.

Reproducir vídeo