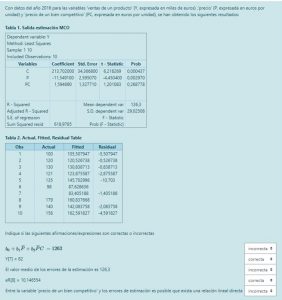
Pregunta 1

a. El modelo tiene una sola variable explicativa — P_{t} — por tanto, es uniecuacional simple.

c. El valor del parámetro \beta_0 es desconocido y, según las hipótesis del MRLNC, constante a lo largo del período muestral. 

d. El modelo tiene 4 variables: el regresando —‘Ventas de un producto’—, dos regresores —el regresor ficticio y la variable ‘precio del bien’— y la perturbación aleatoria. 

Pregunta 2

b. El regresor ficticio, aunque en sentido estricto no es una variable —su valor es uno para todas las observaciones—, se le considera como uno de los regresores del modelo, pero no es una variable explicativa.

c. Se clasificaría como mixto. 

d. En número de regresores, en este caso —modelo con ordenada en el origen—, es igual al número de variables explicativas (k = 2) más uno.

Pregunta 3

a. Se clasificaría como atemporal.

b. Los modelos econométricos son aleatorios.

c. En este caso, la variable explicativa es exógena.

Pregunta 4

a. La mayoría de los modelos incluyen la ordenada en el origen para recoger los efectos fijos que se presentan en algunas de las relaciones entre variables económicas y/o para obtener mejores aproximaciones de la relación entre las variables cuando ésta es no lineal, pero se utiliza una aproximación lineal.
La perturbación aleatoria es la variable que recoge el efecto conjunto de los factores omitidos.

b. Este modelo tiene 2 variables aleatorias: el regresando y la perturbación aleatoria.

d. Se clasificaría como temporal.

Pregunta 5

b. Este modelo tiene 5 variables: V_t; x_{0t}; P_t; V_{t-1}; \varepsilon_{t}

c. Es un modelo dinámico autorregresivo.

d. La perturbación aleatoria es no observable.

Pregunta 6

a. El valor del parámetro \beta_0 es desconocido y, según las hipótesis del MRLNC, constante a lo largo del período muestral. 

c. Este modelo tiene 5 variables: IB_t; x_{0t}; AC_t; SK_{t}; \varepsilon_{t}

d. El modelo no es lineal, pero sí linealizable.

Pregunta 1

a. Un estimador es óptimo si su varianza teórica es mínima entre los estimadores lineales e insesgados de \beta

d. La perturbación aleatoria es una variable no observable.

Pregunta 2

b. Según la hipótesis de homocedasticidad, la varianza de la perturbación es constante. 

c. Para que las varianzas estimadas de los estimadores sean estimadores insesgados de las varianzas de los estimadores es necesario que, entre otras, se cumpla la hipótesis de incorrelación de las perturbaciones.

Pregunta 3

b. Si el modelo es clásico la esperanza matemática de la perturbación — media teórica — es nula y su varianza es contante —hipótesis de homocedasticidad.

d. \frac {E(SCE)}{T – k – 1} = \frac {E(\sum(y_t – \widehat{y}_t)^2)}{T – k -1} = \sigma^2

Pregunta 4

a. Para especificar un modelo econométrico es necesario describir las variables que lo forman desde un punto de vista estadístico.

b. El EMCO (b) es un estimador consistente de  \beta con independencia del tamaño de la muestra.

Pregunta 5

c. Para demostrar que el EMCO(b) es óptimo es necesario asumir, entre otras hipótesis, que X es no estocástica.

d. Para especificar un modelo econométrico es necesario describir las variables que lo forman desde un punto de vista estadístico.

Pregunta 6

a. Para demostrar que el EMCO(b) es consistente de \beta es necesario asumir, entre otras hipótesis, que los parámetros \beta son constantes.

c. Se trata de un modelo dinámico autorregresivo en el que una de las explicativas es la endógena retardada, variable estocástica y, por tanto, se incumple la hipótesis clásica de regresores no estocásticos.

Pregunta 7

a. La hipótesis de incorrelación supone que entre perturbaciones correspondientes a diferentes observaciones no hay relaciones lineales.

c. Si se incumple la hipótesis de regresores no estocásticos, los EMCO (b) dejan de ser óptimos.

Pregunta 8

a. Si el modelo es clásico, el estimador óptimo es el que hace mínima la suma de los cuadrados de los errores de la estimación MCO.

c. Entre las variables explicativas no figura la endógena retardada, por tanto, todas las explicativas son exógenas.

Pregunta 9

a. Hay dos variables aleatorias: el regresando y la perturbación.

b. Para demostrar que el EMCO(b) es óptimo es necesario asumir, entre otras hipótesis, que X es no estocástica.

Pregunta 10

a. Es cierto que el rango de la matriz X es igual al número de regresores de la ecuación —k + 1— pero este es el número de columnas de la matriz X, que tiene T filas.

d. Es cierto que, en este caso, X es estocástica, pero eso no impide que se puedan obtener los EMCO(b).

Pregunta 11

a. Si el modelo es clásico, el estimador óptimo es el que hace mínima la suma de los cuadrados de los errores de la estimación MCO.

c. Es cierto que el rango de la matriz X es igual al número de regresores de la ecuación —k + 1 — pero este es el número de columnas de la matriz X, que tiene T filas.

Pregunta 12

c. Si el modelo es clásico, la expresión E(y_t – Ey_t)(y_s – Ey_s) = E \varepsilon_t  \varepsilon_s =0 \forall t \neq s es correcta.

d. Para demostrar que el EMCO(b) es consistente de  \beta es necesario asumir, entre otras hipótesis, que los parámetros \beta son constantes.

Pregunta 13

c. El EMCO(b) es un estimador consistente de \beta si X es no estocástica, los parámetros son constantes y las esperanzas matemáticas de las perturbaciones son nulas.

d. La hipótesis de rango pleno se incumpliría si, por ejemplo x_{0t} = x_{1t} \forall t .

Pregunta 14

c. Para demostrar que el EMCO(b) es insesgado es necesario asumir que la esperanza matemática de las perturbaciones es nula, que los regresores son no estocásticos y que los parámetros  \beta son constantes.

d. Hay dos variables aleatorias: el regresando y la perturbación.

Pregunta 15

b. Este modelo se clasifica como uniecuacional, múltiple —tiene 2 variables explicativas—, lineal y estático.

d. V(b) tiende a cero cuando T tiende a infinito si el EMCO(b) es un estimador consistente de \beta y para que esto suceda es necesario que X sea no estocástica; los parámetros, constantes y las esperanzas matemáticas de las perturbaciones, nulas.

Pregunta 16

a. En el modelo clásico se supone que los regresores son no estocásticos, son fijos en el muestreo.

b. Que X sea estocástica, no impide que se puedan obtener los EMCO(b). Los EMCO(b) no pueden obtenerse cuando el rango de X no es pleno.

Pregunta 17

b. Si las esperanzas de las perturbaciones son nulas, la matriz de varianzas-covarianzas del vector de perturbaciones es escalar, los regresores son no estocásticos y los coeficientes \beta son constantes a lo largo de la muestra, el EMCO(b) es óptimo y, por tanto, el más eficiente.

c. La expresión correcta es: E(y_t – Ey_t)^2 = E \varepsilon_t^2 = \sigma ^2 \forall t

Pregunta 1

b. S_{b_{0}} = \sqrt {81235,84884} = 285,019032 es la desviación típica estimada de b_{0}

d. La suma de cuadrados de errores siempre disminuye al incorporar regresores adicionales al modelo y, por tanto, la raíz del error cuadrático medio — RECM = \sqrt{SCE/T} — también.

e. El método de mínimos cuadrados ordinarios consiste en minimizar la suma de cuadrados de errores, pero eso no garantiza que el ajuste sea bueno.

Pregunta 2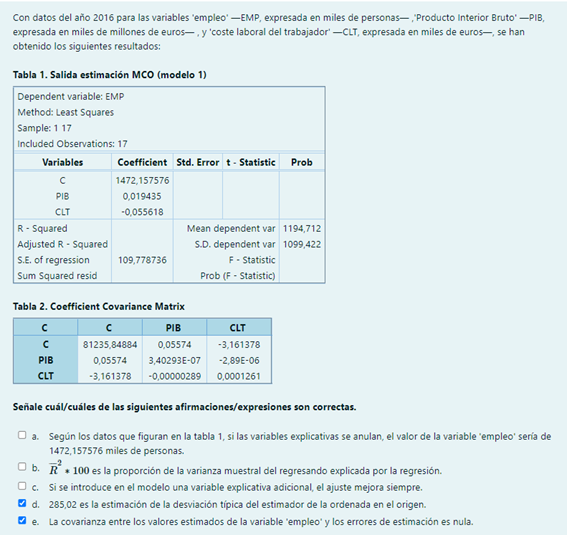

a. Según los datos que figuran en la tabla 1, si las variables explicativas se anulan, se estima que por término medio el valor de la variable ‘empleo’ sería de 1472,157576 miles de personas.

b. R^2 * 100 es la proporción de la varianza muestral del regresando explicada por la regresión.

c. Si se introduce una variable explicativa adicional, el ajuste mejora si dicha variable es relevante en la explicación del comportamiento del regresando.

Pregunta 3

b. En la columna ‘Std.Error’ figuran las desviaciones típicas estimadas de los estimadores MCO.

d. Según los datos que figuran en la tabla 1, si la variable ‘coste laboral por trabajador’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que por término medio la variable ‘empleo’ disminuye 0.055618 miles de personas.

e. El primer elemento de la matriz de varianzas-covarianzas estimada de los estimadores — \widehat {V}(b) — es la varianza estimada de b_0 .

Pregunta 4

b. Por término medio, el porcentaje de error que se comete al estimar los valores de la variable ‘empleo’ utilizando la regresión que figura en la tabla 1, es del 8,34%.

c. Según los datos que figuran en la tabla 1, si las variables explicativas se anulan, se estima que por término medio el valor de la variable ‘empleo’ sería de 1227,375395 miles de personas.

e. Al eliminar la variable ‘número de empresas’ del modelo de la tabla 1, el ajuste empeora.
\overline{R}_{Modelo1} = 0,989263 > \overline{R}_{Modelo2}=0,987123 = 1- \frac{16}{14}(1-0,988733)  

Pregunta 5

a. \sum (EMP_t – \widehat{EMP}_t )= 0 por propiedades del ajuste MCO.

b. Por las propiedades del ajuste MCO, los errores de la estimación están incorrelacionados con los valores estimados del regresando.

c. Según los datos que figuran en la tabla 1, si la variable ‘número de empresas’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que, por término medio, la variable ‘empleo’ se incrementa en 0,000473 miles de personas.

Pregunta 6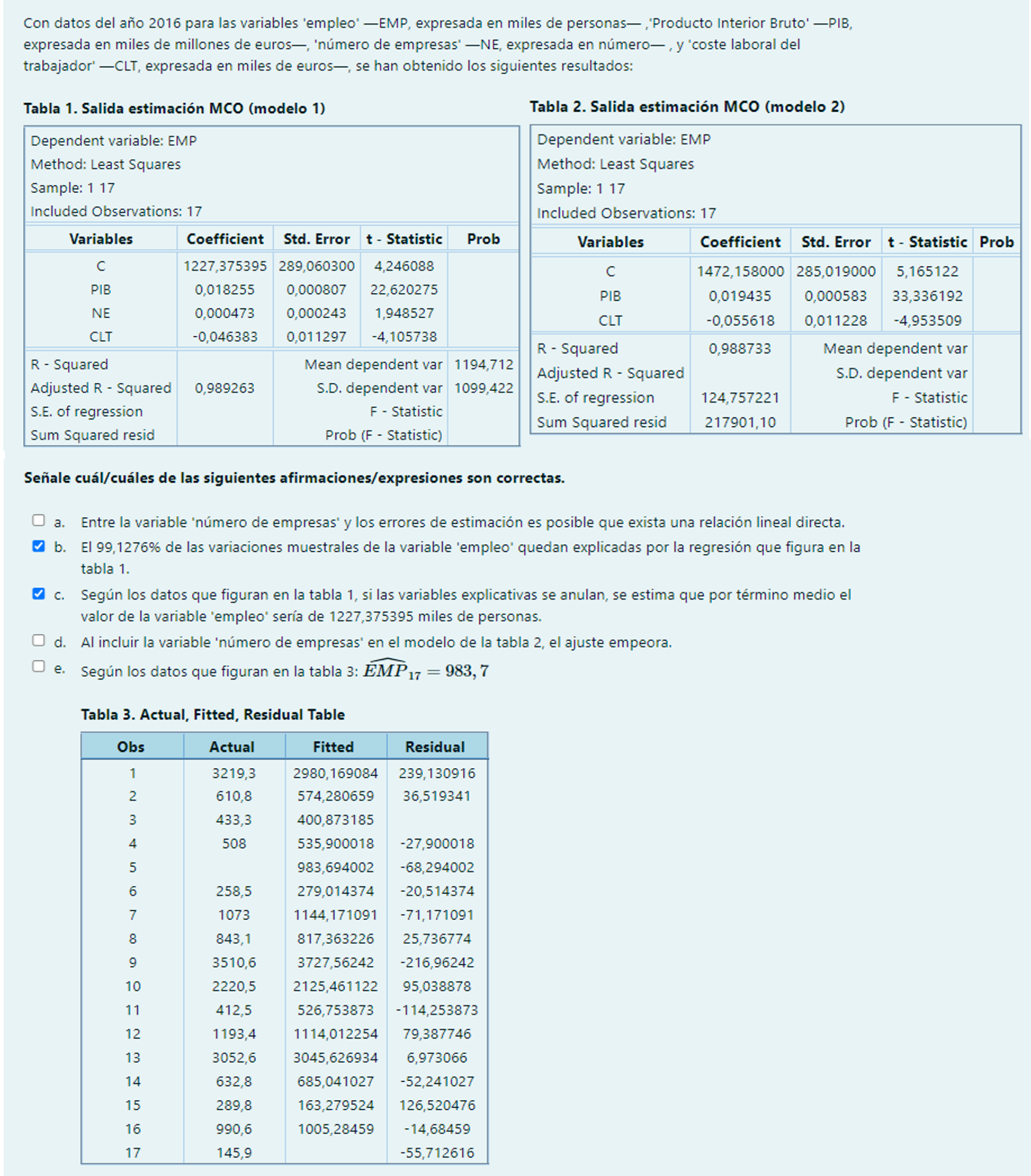

a. Por propiedades del ajuste MCO entre las variables explicativas y los errores de estimación, no existe correlación muestral.

d. Al incluir la variable ‘número de empresas’ en el modelo de la tabla 2, el ajuste mejora: 
\overline{R}_{Modelo1} = 0,989263 > \overline{R}_{Modelo2}=0,987123 = 1- \frac{16}{14}(1-0,988733)  

e. \widehat{EMP}_{17} = EMP_{17} – e_{17} = 201,612616

Pregunta 7

a. \sum (EMP_t – \widehat{EMP}_t )= 0 por propiedades del ajuste MCO.

b. Por las propiedades del ajuste MCO, los errores de la estimación están incorrelacionados con los valores estimados del regresando.

c. Según los datos que figuran en la tabla 1, si la variable ‘número de empresas’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que, por término medio, la variable ‘empleo’ se incrementa en 0,000473 miles de personas.

Pregunta 8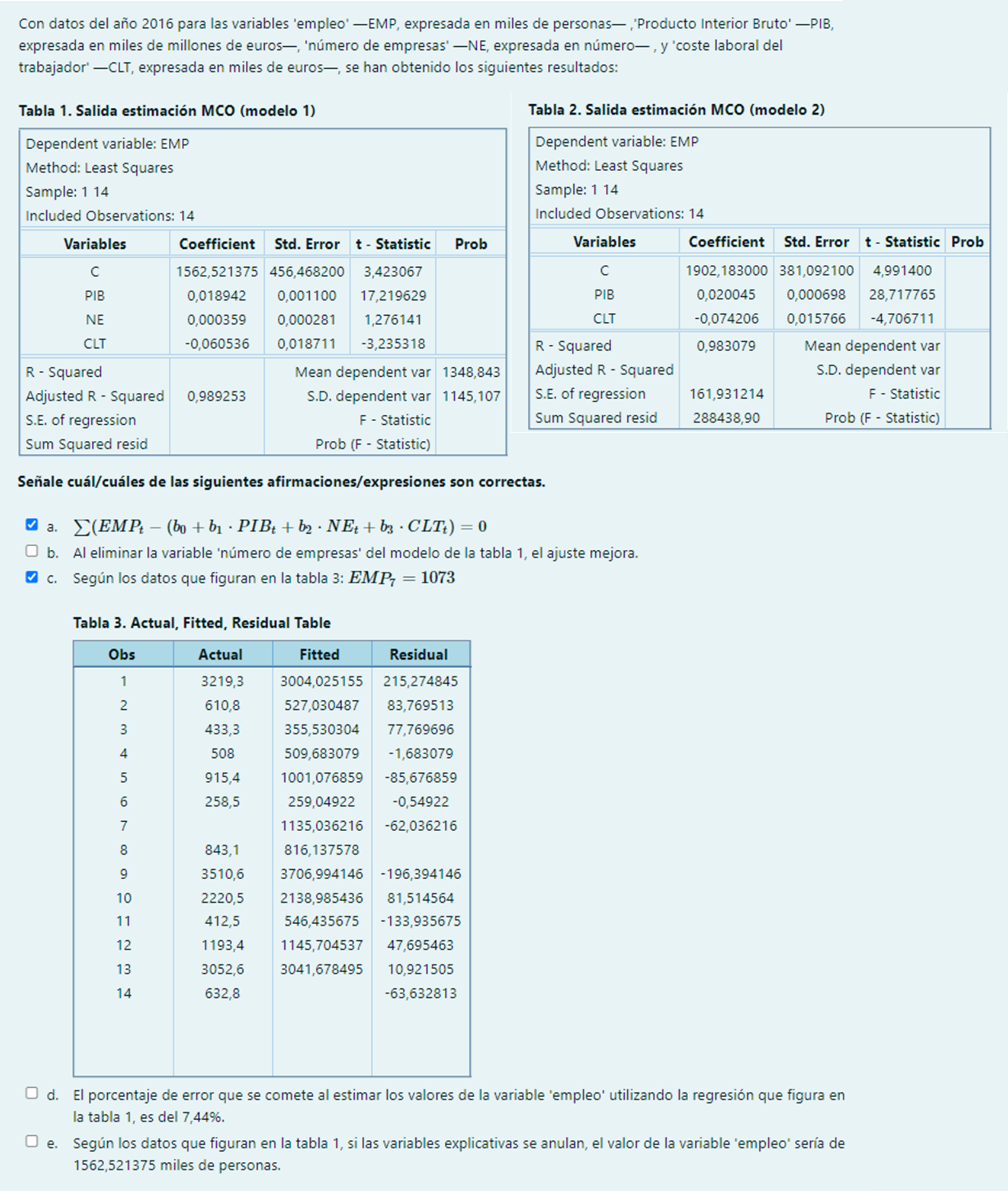

b. Al eliminar la variable ‘número de empresas’ del modelo de la tabla 1, el ajuste empeora.
\overline{R}_{Modelo1} = 0,989253 > \overline{R}_{Modelo2}=0,98 = 1- \frac{13}{11}(1-0,983079)  

d. Por término medio, el porcentaje de error que se comete al estimar los valores de la variable ‘empleo’ utilizando la regresión que figura en la tabla 1, es del 7,44%.

e. Según los datos que figuran en la tabla 1, si las variables explicativas se anulan, se estima que por término medio el valor de la variable ‘empleo’ sería de 1562,521375 miles de personas.

Pregunta 9

a. Es cierto que la suma de los valores estimados del regresando es 20310,104 pero el primer elemento de la matriz X^{\prime} X es 17 (= T)

b. SCT_{Modelo2} = SCT_{Modelo1} = 1099,422^2 (17-1)=19339659,75

e. Según los datos que figuran en la tabla 1, si la variable ‘coste laboral del trabajador’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que, por término medio, la variable ‘empleo’ disminuye 0.055618 miles de personas.

Pregunta 10

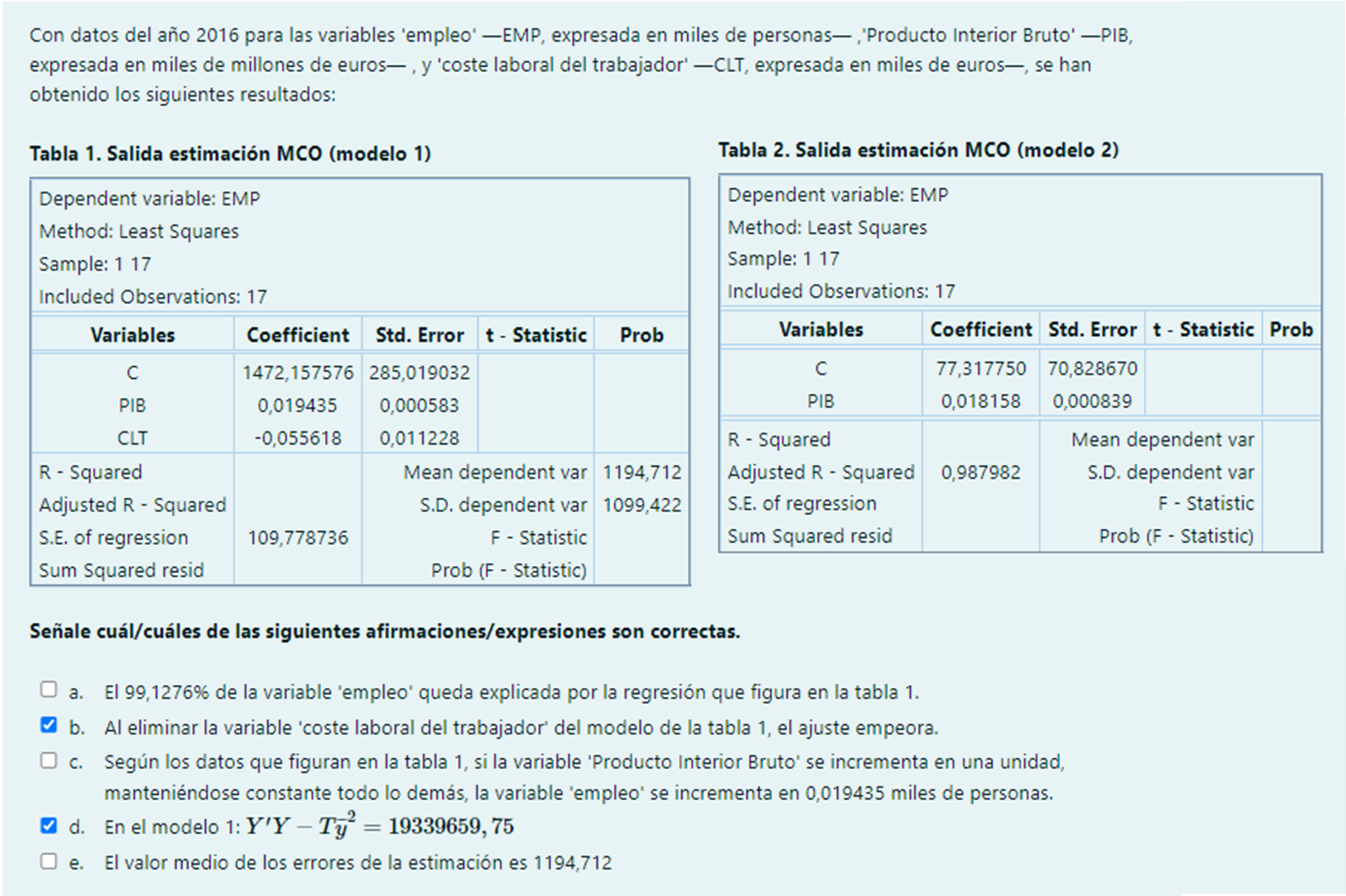
a. El 99,1276% de las variaciones muestrales de la variable ‘empleo’ quedan explicadas por la regresión que figura en la tabla 1.

c. Según los datos que figuran en la tabla 1, si la variable ‘Producto Interior Bruto’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que, por término medio, la variable ‘empleo’ se incrementa en 0,019435 miles de personas.

e. El valor medio de los errores de la estimación es cero por las propiedades del ajuste MCO.

Pregunta 1

a. Al incorporar un nuevo regresor al modelo siempre disminuye la variabilidad muestral del error — SCE/ T   —. La variabilidad muestral del regresando — SCT/ T     — no cambia. El valor del coeficiente de determinación corregido aumenta siempre y cuando el regresor adicional sea relevante para la explicación del comportamiento del regresando.

d. Si el modelo es clásico, V(b) tiende a cero a medida que T aumenta.

f. El primer elemento de la matriz  X ^{\prime} X es T = 17

Pregunta 2

b. R^2 *100 es la proporción de la varianza muestral del regresando explicada por la regresión.

c. Los EMCO(b) son lineales en Y si X es no estocástica.

d. La matriz  X ^{\prime} X es cuadrada de orden 4 (= k + 1)

Pregunta 3

a. Según los datos que figuran en la tabla 1, si la variable ‘índice de precios del producto’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que, por término medio, la variable ‘ventas de una empresa’ disminuye 0,525206 miles de euros constantes de 2005.

d. \sum( V_t – \widehat{V_t} ) = 0

f. SCT = 28,72892^2 (17-1) ;;   SCE = 1,014908^2 (17-3-1);; \sum {( \widehat {y}_t – \overline {\widehat {y}} )} ^2 = SCR = SCT – SCE = 13192,223

Pregunta 4

d. Si este modelo es clásico, se supone que los valores de son los mismos para todas las observaciones muestrales (hipótesis de homocedasticidad).

e. Según los datos que figuran en la tabla 1, si las variables explicativas se anulan, se estima que por término medio el valor de la variable ‘ventas de una empresa’ sería de 3,63858 miles de euros constantes de 2005.

f. \sum( V_t – \widehat{V_t} ) = 0

Pregunta 5

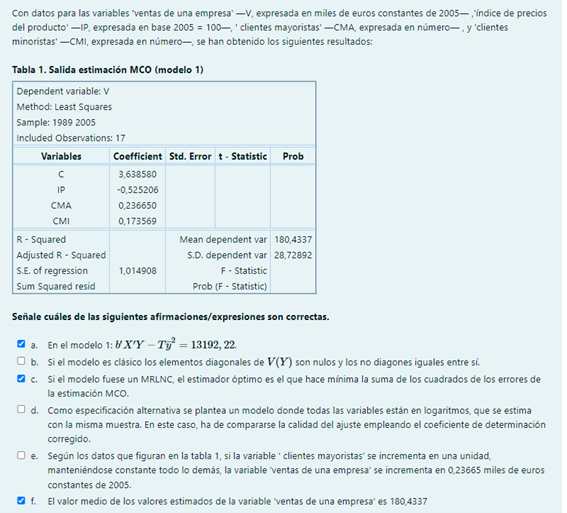
b.  Si el modelo es clásico, los elementos no diagonales de la matriz V(Y) = V( \varepsilon ) = \sigma^2 I son ceros y los diagonales iguales entre sí.

d. En este caso, el regresando del modelo alternativo se ha transformado en logaritmos por lo que para comprar la bondad de los ajustes ha de tenerse en cuenta que los modelos tienen dos variables explicativas diferentes. 

e. Según los datos que figuran en la tabla 1, si la variable ‘clientes mayoristas’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que, por término medio, la variable ‘ventas de una empresa’ se incrementa en 0,23665 miles de euros constantes de 2005.

Pregunta 6

a. El primer elemento de la matriz  X ^{\prime} X es T = 16

d. Al incorporar un nuevo regresor al modelo siempre disminuye la variabilidad muestral del error — SCE/ T   —. La variabilidad muestral del regresando — SCT/ T     — no cambia. El valor del coeficiente de determinación corregido aumenta siempre y cuando el regresor adicional sea relevante para la explicación del comportamiento del regresando.

e. Si el modelo es clásico, V(b) tiende a cero a medida que T aumenta.

Pregunta 7

b. \sum e_{t}^{2} = SCE =  \frac{10 -3 – 1}{10 – 1} 12,5526^2 (10 – 1)(1-0,971337) = 27,0981894

c. El 98,0891% de las variaciones muestrales de la variable ‘ventas de un producto’ quedan explicadas por la regresión que figura en la tabla1.

e. En el MRLNC, se supone que los valores de los regresores son fijos en el muestreo.

Pregunta 8

b. Por término medio, el porcentaje de error que se comete al estimar los valores de la variable ‘ventas de un producto’ utilizando la regresión que figura en la tabla 1 es del 2,64%.

c. En la columna ‘Std.Error’ figuran las desviaciones típicas estimadas de los estimadores MCO.

d. Si el modelo es clásico, la perturbación aleatoria, que se incorpora al modelo teórico para recoger los efectos de las variables omitidas, tiene media teórica nula — E \varepsilon {_t} = 0 \forall t — y varianza constante — E \varepsilon_t^2 = \sigma^2 \forall t —

Pregunta 9

a. b_0 + b_1 \overline {P} + b_2 \overline {GP} + b_3 \overline {IC} = \overline {V} = 62,3 por las propiedades del ajuste MCO.

b. Según los datos que figuran en la tabla 1, si las variables explicativas se anulan, se estima que por término medio el valor de la variable ‘ventas de un producto’ sería de 13,2556 miles de unidades físicas.

f. La expresión S^2 x^{ii} que representa la varianza estimada del estimador b_i, proporciona por término medio una estimación exacta de \sigma^2 x^{ii} si el modelo es clásico.

Pregunta 10

a. Según los datos que figuran en la tabla 1, si la variable ‘gastos en publicidad’ se incrementa en una unidad, manteniéndose constante todo lo demás, se estima que, por término medio, la variable ‘ventas de un producto’ se incrementa en 0,205745 miles de unidades físicas.

b. Si el modelo es clásico, los elementos diagonales de \widehat {V}(b) — varianzas estimadas de los estimadores— proporcionan por término medio, estimaciones exactas de los elementos diagonales de V(b) — varianzas teóricas de los estimadores —.

c. Para que se cumplan todas las propiedades del ajuste MCO es necesario que el modelo tenga ordenada en el origen y se haya estimado por MCO.

Pregunta 11

a. El 99,41% de las variaciones muestrales de la variable ‘ventas de un producto’ quedan explicadas por la regresión que figura en la tabla.

b. Las medidas evaluadoras de la calidad del ajuste proporcionan la misma información: el ajuste es bueno.
R^2 = 1- \frac {1,049302^2 (33-3-1)}{13,0278768^2(33-1)} = 0,994121 > 0,9
% RECM = \frac {\sqrt {1,049302^2 (33-3-1)/33}}{66,37056} = 1,482% < 5%

c. Al incluir en el modelo una variable explicativa adicional, siempre aumenta el valor de R^2, pero eso no significa que el ajuste mejore. El ajuste mejora si la variable explicativa adicional es relevante en la explicación del comportamiento del regresando.

Pregunta 12

a. \overline {R} ^2= 1 – \frac {SCE/(T – k- 1)}{SCT/ (T-1)} puede ser negativo, aunque el modelo tenga ordenada el origen.

b. Las medidas evaluadoras de la calidad del ajuste proporcionan la misma información: el ajuste es bueno.
R^2 = 1- \frac {1,59601^2 (15-3-1)}{19,18258^2(15-1)} = 0,994560 > 0,9
% RECM = \frac {\sqrt {1,59601^2 (15-3-1)/15}}{73,4} = 1,86% < 5%

Pregunta 13

a. V(b) es una matriz cuadrada de orden 2 y simétrica, pero no es ni diagonal ni escalar. 

d. Si la variable ‘renta total de su área’ se incrementa en mil euros, se estima que, por término medio, la variable ‘ventas de gasolina’ se incrementa en 0.0563819 miles de euros.

Pregunta 14

a. Por término medio, el porcentaje de error que se comete al estimar los valores de la variable ‘empleo’ utilizando la regresión que figura en la tabla 1, es del 6,62%.

d. Al incorporar la variable ‘número de empresas’ el ajuste mejora.
\% ES_{Modelo1} = \frac {\sqrt{80948,17/(10-2-1)}}{1359,25}*100 = 7,9 \% < \% ES_{Modelo2} = \frac{192,353321}{1359,25}*100 = 14,1514 \%

Pregunta 1

c. Al nivel de significación del 15%, la hipótesis nula  H_{0}: \beta_1 = \beta_2 = \beta_3 = \beta_4 = 0 se rechaza porque F = 282,870816 > 1,7223 , por tanto, la probabilidad asociada al estadístico de prueba es inferior al 15%.

d. Al nivel de significación del 15%, la hipótesis nula  H_{0}: \beta_1 = \beta_2 = \beta_3 = \beta_4 = 0 se rechaza porque F = 282,870816 > 1,7223 , por tanto, la probabilidad de rechazar la hipótesis nula siendo cierta es inferior al 15%.

Pregunta 2

a. \lvert t_1 \lvert = 1,61142 < 2,6226 \rightarrow NRH_{0}: \beta_1 = 0 , por tanto, el intervalo de confianza del 99% para este parámetro sí contiene el valor cero. 

d.  \lvert t_3 \lvert = 1,04031 < 1,9824 \rightarrow NRH_{0}: \beta_3 = 0 , por tanto, la probabilidad asociada al estadístico de prueba es superior al 5%.

Pregunta 3

a.  El 91,3604% de las variaciones muestrales de la variable ‘tasa de morosidad de una entidad financiera’ quedan explicadas por esta regresión.
R^2 = \frac {282,870816*4/107}{1+(282,870816*4/107)} = 0,913604

b. \lvert t_1 \lvert = 1,61142 < 2,6226 \rightarrow NRH_{0}: \beta_1 = 0 . Al nivel de significación del 1%, la información muestral es compatible con un valor de este parámetro igual a cero.

Pregunta 4

a. El 91,3604% de las variaciones muestrales de la variable ‘tasa de morosidad de una entidad financiera’ quedan explicadas por esta regresión.
R^2 = \frac {282,870816*4/107}{1+(282,870816*4/107)} = 0,913604

d. \lvert t_1 \lvert = 1,61142 < 2,6226 \rightarrow NRH_{0}: \beta_1 = 0 . Al nivel de significación del 1%, la hipótesis nula H_0: \beta_1 = 0 no se rechaza.

Pregunta 5

b. Prob(t_3)=0,000180 < 0,10 . Al nivel de significación del 10%, la variable ‘tipo de interés’ es individualmente relevante.

c. F= \frac{0,98312/4}{(1-0,98312)/103} = 1499,7239
Este valor es coherente con los valores de las probabilidades asociadas a los estadísticos t porque son indicativos de que las variables TVPIB, TI y VCC son individualmente relevantes prácticamente a cualquier nivel de significación, por tanto, también lo son conjuntamente.

Pregunta 6

b. F= 1499,7239 > 1,7237 Al nivel de significación del 15% la hipótesis nula H_0: \beta_1 = \beta_2 = \beta_3 = \beta_4 = 0 se rechaza. Por tanto, la probabilidad asociada a este estadístico F es inferior al 15%.

d. F= 1499,7239 > 1,7237 Al nivel de significación del 15% la hipótesis nula H_0: \beta_1 = \beta_2 = \beta_3 = \beta_4 = 0 se rechaza. Por tanto, la probabilidad asociada a este estadístico F es inferior al 15%.

Pregunta 7

b. 1- R^2 = 1 – \frac {190,24306*4/105}{1+(190,24306*4/105)} = 0,121251
El 12,1251% de las variaciones muestrales de la variable ‘tasa de morosidad de una entidad financiera’ no quedan explicadas por esta regresión.

c. \lvert t_2 \lvert = 1,803921 < 1,9824 \rightarrow NRH_{0}: \beta_2 = 0 , por tanto, la probabilidad asociada al estadístico de prueba es superior al 5%.

Pregunta 8

a. \lvert t_3 \lvert = 1,040312 < 1,9824 \rightarrow NRH_{0}: \beta_3 = 0 , por tanto, la probabilidad asociada al estadístico de prueba es superior al 5%.

d. \lvert t_1 \lvert = 1,6114125 < 2,6226 \rightarrow NRH_{0}: \beta_1 = 0 , el intervalo de confianza del 99% para el parámetro  contiene el cero.

Pregunta 9

c. Al rechazarse al menos una de las hipótesis de nulidad individual de uno de los coeficientes angulares del modelo, la hipótesis de nulidad conjunta de los coeficientes angulares del modelo se rechaza.

d. F= \frac{0,98312/4}{(1-0,98312)/103} = 1499,7239
El estadístico F de la tabla 1 se utiliza para contrastar la hipótesis de relevancia conjunta de todas las variables explicativas del modelo.

Pregunta 10

b. Prob(t_3)=0,000180 < 0,10 . Al nivel de significación del 10% la hipótesis nula H_0: \beta_3 = 0 se rechaza , por tanto el valor de \lvert t_3 \lvert es superior al punto crítico correspondiente a una t de Student con 103 grados de libertad.

c. Prob(t_1)=0,000178 < 0,10 . La probabilidad de equivocarse al afirmar que la hipótesis H_0: \beta_1 = 0 es falsa es muy pequeña.

Pregunta 11

a. F = \frac {0,987976/4}{(1 – 0,987976)/105} = 2156,88373

c. Al rechazarse al menos una de las hipótesis de nulidad individual de uno de los coeficientes angulares del modelo, la hipótesis de nulidad conjunta de los coeficientes angulares del modelo se rechaza.

Pregunta 1

b. En este caso, el valor del estadístico F es alto y su probabilidad asociada es baja. 
F= \frac{0,826033/3}{(1-0,826033)/(25-3-1)}= 33,2375

Pregunta 2

a. El intervalo de confianza del 99% para el parámetro \beta_2 contiene el valor cero.
Prob(t_2) = 0,4958 > 0,01 \rightarrow NRH_{0}: \beta_2 =0

b. La probabilidad de cometer un error al afirmar que la variable ‘índice de precio de los coches usados’ es individualmente relevante es del 0,75%.

d. F = \frac{0,998178/4}{(1-0,998179)/(33-4-1)} = 3837,04174

Pregunta 3

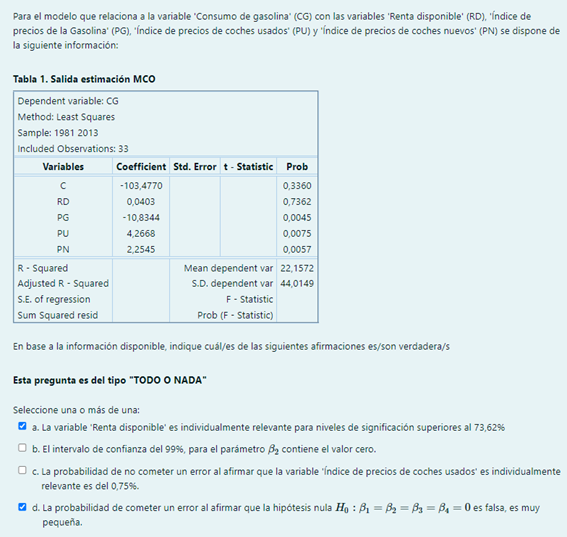
b. El intervalo de confianza del 99% para el parámetro \beta_2   no contiene el valor cero.
Prob(t_2) = 0,0045 < 0,01 \rightarrow RH_{0}: \beta_2 =0

c. La probabilidad de cometer un error al afirmar que la variable ‘índice de precio de los coches usados’ es individualmente relevante es del 0,75%.

Pregunta 4

b.  t_1 = \frac {0,2543 – 0,24}{0,2543/423,833333} = 23,8333 > 1,7109 \rightarrow RH_{0}: \beta_1 = 0,24

c. El intervalo de confianza del 95% para \beta_3 no contienen valores negativos:
(0,0006  \mp \frac {0,0006}{3}2,0639) = (0,00018722; 0,00101278)

d. t_1 = 423,8333  \rightarrow RH_{0}: \beta_1 = 0 a cualquiera de los niveles de significación habituales.  Por tanto, el valor del estadístico F es alto y su probabilidad asociada baja dado que la hipótesis nula H_{0}: \beta_1 = \beta_2 = \beta_3 = 0  se rechaza a cualquiera de los niveles de significación habituales.

Pregunta 5

a. Prob(t_2) = 0,0022 \rightarrow la hipótesis nula H_0: \beta_2 =0 se rechaza para niveles de significación superiores al 0,22%. Por tanto, los intervalos para niveles de confianza inferiores al 99,78% no contienen el valor cero.

c. Prob(t_3) = 0,2403 > 0,05 \rightarrow NRH_0: \beta_3=0 Por tanto, el valor del estadístico t_3 es inferior al del punto crítico correspondiente a una distribución t de Student con 12 (=16-3-1) grados de libertad.

Pregunta 6

a. Prob(t_1) = 0,0007 \rightarrow la hipótesis nula H_0: \beta_1 = 0 se rechaza para niveles de significación superiores al 0,07% y puede concluirse que la variable ‘Superficie útil’ es individualmente relevante.

Pregunta 7

a. La probabilidad de que el valor 1,2173 ( b_0 ) esté dentro del intervalo de confianza del 90% para el parámetro \beta_0 es igual a uno porque b_0 es el centro del intervalo.

c. El intervalo de confianza del 90% para el parámetro \beta_1 :
(0,2648  \mp \frac {0,2648}{1,143844}1,7011) = (-0,129; 0,6586)

d. El intervalo de confianza del 95% para el parámetro \beta_3 :
(0,0020  \mp \frac {0,0020}{0,056180}2,0484) = (-0,07292; 0,07492)

Pregunta 8

a.  La probabilidad de que el valor 129,062 (   = b_0 ) esté dentro del intervalo de confianza del 90% para el parámetro \beta_0 es igual a uno porque b_0 es el centro del intervalo.

Pregunta 9

a. Prob(t_1) = 0,0001 \rightarrow la hipótesis nula H_0: \beta_1 =0 se rechaza para niveles de significación superiores al 0,01%. Por tanto, los intervalos para niveles de confianza inferiores al 99,99% no contienen el valor cero.

b. La hipótesis nula H_{0}: \beta_2 = 0 se rechaza para niveles de significación superiores al 9,54%.

d. El estadístico F que figura en la tabla se utiliza para contrastar la hipótesis de relevancia conjunta de todas las variables explicativas del modelo.

Pregunta 10

d. En este caso, la probabilidad asociada al estadístico F que debería figurar en la tabla, es baja porque:
\lvert t_2  \lvert = 423,833333 > 2,7969 \rightarrow RH_{0}: \beta_1=0 al nivel de significación del 1%
\lvert t_3  \lvert = 3,000 > 2,7969 \rightarrow RH_{0}: \beta_3=0 al nivel de significación del 1%

Por tanto, se rechaza la hipótesis nula H_{0}: \beta_1 = \beta_2 = \beta_3 = 0 por lo que el valor del estadístico F es alto y su probabilidad asociada baja.

Pregunta 1

a. Prob(F) = 0,0029<0,01 Al nivel de significación del 1%, la hipótesis nula H_0: \beta_2 = 2 \beta_1 se rechaza.

d. El valor del estadístico F de la tabla 1 permite contrastar la hipótesis de nulidad conjunta de los coeficientes angulares del modelo, mientras que el estadístico F que figura en la tabla 3 se utiliza para contratar la hipótesis nula H_0: \beta_2 = 2 \beta_1

Pregunta 2

a. F= \frac{(306,032314-238,40626)/(3-1)}{238,40626/36}=5,10586>3,2594 \rightarrow RH_{0}: \beta_1 =\beta_3 =0 por tanto, el incremento que se produce en SCE al eliminar del modelo las variables ‘Precio de gasolina’ y ‘Población’ sí es estadísticamente significativa.

c. La restricción que se establece en la tabla 3 es \beta_2 = 2 \beta_1 . El modelo con esta restricción es: TUA_{t} = \beta_0+ \beta_1 (PG_{t} +2S_{t})+\beta_3 POB_{t} + \varepsilon_{t}

Pregunta 3

b. SCE_{R} = 238,40626(1+10,229 \frac{1}{36})=306,1

c. La restricción que se establece en la tabla 3 es \beta_2 = 2 \beta_1 . El modelo con esta restricción es: TUA_{t} = \beta_0+ \beta_1 (PG_{t} +2S_{t})+\beta_3 POB_{t} + \varepsilon_{t}

Pregunta 4

c. El estadístico F que ha de utilizarse para contrastar la hipótesis  H_0: \beta_1 = \beta_2 =0, sigue una distribución F de Snedecor con k – k_{R} = 4 – 2  grados de libertad en el numerador y T – k – 1 = 70 – 4 – 1 en el denominador.

d. F= \frac{(2607,093855-2277,718)/1}{2277,718/65}=9,39951

Pregunta 5

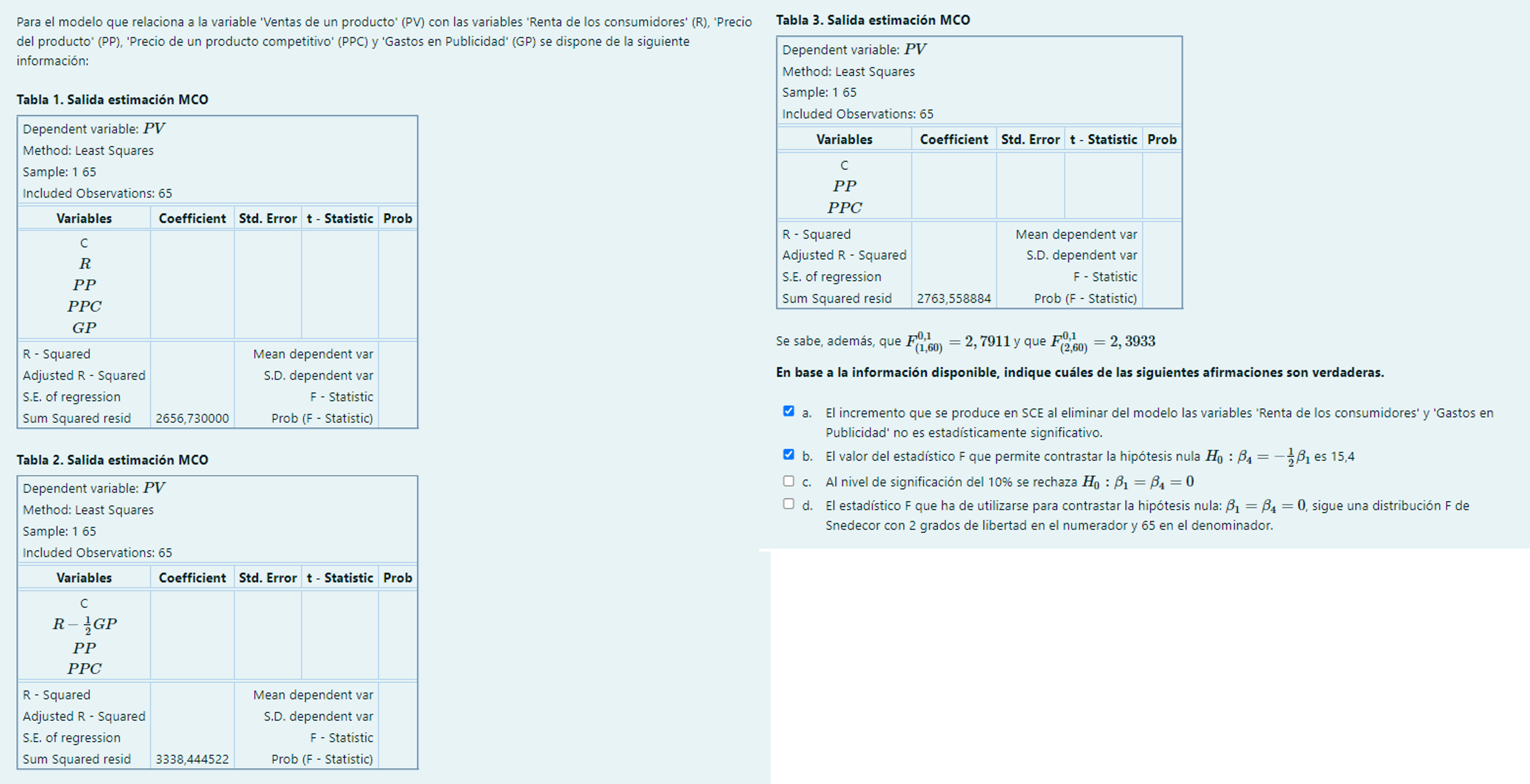
c.  F= \frac{(2763,558884-2656,73)/2}{2656,73/60}=1,20632<2,3933 \rightarrow NRH_{0}: \beta_1=\beta_4=0

d. El estadístico F que ha de utilizarse para contrastar la hipótesis  H_0: \beta_1 = \beta_4 =0, sigue una distribución F de Snedecor con k – k_{R} = 4 – 2  grados de libertad en el numerador y T – k – 1 = 65 – 4 – 1 en el denominador.

Pregunta 6

a.  Al nivel de significación del 10%  ninguna de las variables ‘Renta de los consumidores’ y ‘Precio de un producto competitivo’ se muestran individualmente relevantes.
F= \frac{(2358,295312-2459,935)/2}{2459,935/67}=1,06713<2,3836 \rightarrow NRH_{0}: \beta_1=\beta_3=0

b.  F= \frac {(2358,295312-2459,935)/2}{2459,935/67} = 1,06713

Pregunta 7

b.  La hipótesis nula H_{0}: \beta_3 = 2 \beta_1 se rechaza para niveles de significación superiores al 4,34%.

c.  Al nivel de significación del 1%, la hipótesis nula H_{0}: \beta_2 =  \beta_3 = 0 no se rechaza — Prob(F) = 0,0867 > 0,01—

Pregunta 8

a. SCE_{R} = 4259,112 (1 + 90,225 \frac{1}{180-3-1}) = 6442,51189

d. GCN_{t} = \beta_0 + \beta_1 RD_{t} + \beta_2 (IPR_{t} – \frac{1}{2} IPCN_{t}) + \varepsilon_{t}

Pregunta 1

a. El valor del error relativo correspondiente a  la observación 17 es indicativo de una mala capacidad predictiva: eR_{17} = \frac{182,1952}{207,04} *100 = 88 % > 5%.

c. Por término medio, el porcentaje de error que se comete al predecir los valores de la variable ‘Ventas de una empresa’ utilizando este modelo es del 55%.

Pregunta 2

Pregunta 3

Pregunta 4

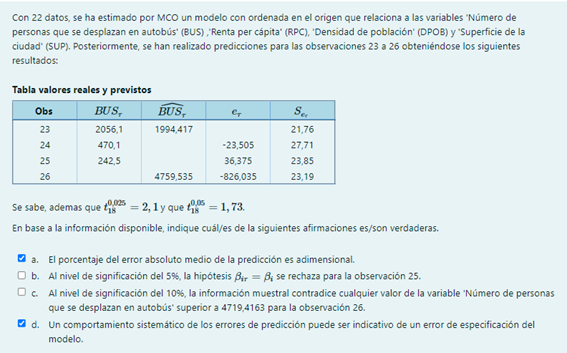
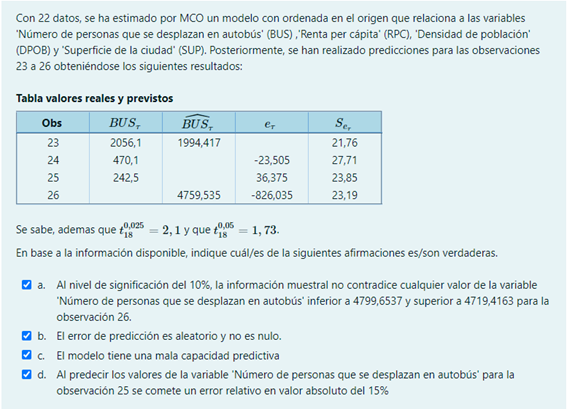
b. Al nivel de significación del 5%, la hipótesis H_{0}: \beta_{i25} = \beta_{i} \forall i no se rechaza. t_{25}= \frac{36,375}{23,85}=1,5252 < 2,1

c. Al nivel de significación del 10%, la información muestral contradice cualquier valor de la variable ‘Número de personas que se desplazan en autobús’ superior a 4799,6537 para la observación 26.  El extremo superior del intervalo de confianza es: 4799,535+(1,73*23,19)=4799,6537

Pregunta 5

b. Al nivel de significación del 5%, la diferencia que hay entre las dos sumas de cuadrados de errores es estadísticamente significativa. F= \frac{(33,87-7,64)/4}{7,64/(15-3-1)} =9,44 > 3,36 La hipótesis nula H_{0}: \beta_{i \tau} = \beta_{i} \forall i \forall \tau se rechaza.

c. Cuanto mayor es la varianza teórica de la perturbación, mayor es la varianza teórica del error de predicción.

Pregunta 6

c. La hipótesis de estabilidad postmuestral para el conjunto de las observaciones extramuestrales se rechaza prácticamente a cualquier nivel de significación — Prob(F – Tabla 3) = 0,0000 —

d. No hay evidencias contrarias a la hipótesis nula H_{0}:  \beta_{i56}= \beta_{i} \forall i
S_{e_{56}} = \frac{\widehat {Qd}_{56} – Extremo Inferior IC}{t_{50}^{0,05}}=23,7202381
t_{56} = \frac{-31,93}{23,7202381}=-1,3461 ; \lvert{t_{56}} \lvert < 2,01 \rightarrow NRH_{0}

Pregunta 7

a. Por término medio, el porcentaje de error que se comete al predecir los valores de la variable ‘Cantidad demandada de un bien’ utilizando este modelo es del 23,5%.

b. La hipótesis nula H_{0}:  \beta_{i55}= \beta_{i} \forall i se rechaza al nivel de significación del 5%.
S_{e_{55}} = \frac{\widehat {Qd}_{55} – Extremo Inferior IC}{t_{50}^{0,05}}=21,7619048
t_{55} = \frac{908,13}{21,7619048}=41,73 ; \lvert{t_{55}} \lvert > 2,01 \rightarrow RH_{0}

Pregunta 8

a. SCE_{54+4} = (14,549988 \frac{4}{50}+1)*2507,21 = 5425,6

d. Al nivel de significación del 10%, la información muestral contradice cualquier valor de la variable ‘Cantidad demandada de un bien’ superior a 3190,79 e inferior a 3097,59 para la observación 58.
S_{e_{58}} = \frac{\widehat {Qd}_{58} – Extremo Inferior IC}{t_{50}^{0,05}}=27,7380952
\widehat {Qd}_{58} + 1,68*27,7380952 =3190,79

Pregunta 9

b. Al nivel de significación del 10%, la información muestral contradice cualquier valor de la variable ‘Cantidad demandada de un bien’ inferior a 1588,58 para la observación 56.

d. La hipótesis de que las variables explicativas tienen en la explicada los mismos efectos para el conjunto de las observaciones muestrales se rechaza prácticamente a cualquier nivel de significación — Prob(F – Tabla 3) = 0,0000 —

Pregunta 10

b. Por término medio, el porcentaje de error que se comete al predecir los valores de la variable ‘Cantidad demandada de un bien’ utilizando este modelo es del 23,5%.

c. La hipótesis nula H_{0}: \beta_{i57} = \beta_i \forall i se rechaza al nivel de significación del 5%. El modelo no es apropiado para predecir los valores de la variable ‘Cantidad demandada de un bien’ para la observación 57.

S_{e_{57}} = \frac{\widehat {Qd}_{57} – Extremo Inferior IC}{t_{50}^{0,05}}=25,75 ; t_{57} = \frac{175,27}{25,75}=6,81 ; \lvert{t_{57}} \lvert > 2,01 \rightarrow RH_{0}

Pregunta 11

b. Sí hay evidencias contrarias a que los parámetros del modelo con el que se han obtenido estos resultados para el conjunto de las observaciones extramuestrales sean los mismos que en el período muestral — Prob(F – Tabla 3) = 0,0000 —

d. Al nivel de significación de 10%, la información muestral contradice cualquier valor de la variable ‘Cantidad demandada de un bien’ inferior a 1588,58 y superior a 1668,28 para la observación 56.

Pregunta 1

a. FIV_{R} = \frac{1}{1-0,9548} = 22,12

c. Los elementos de la matriz de correlación —R_X — son los coeficientes de correlación lineal entre las variables explicativas del modelo.

Pregunta 2

c. FIV_{3} = \frac{1}{1-0,9548} = 22,12
Puede concluirse, por tanto, que la variable ‘Renta disponible per cápita’ es altamente colineal con los restantes regresores del modelo.

Pregunta 3

c. La multicolinealidad no ocasiona el incumplimiento de la hipótesis de rango pleno.

Pregunta 4

c. La matriz de varianzas-covarianzas de los estimadores V(b) = \sigma^{2} (X ^{\prime} X)^{-1} no es una matriz escalar.

d. Si R_{INV}^{2} estuviese próximo a uno, sería posible que S_{b_{1}}^{2}=\frac {S^{2}}{\sum{(INV_{t} – \overline{INV})^{2} (1-R^{2}_{INV})}} tomase un valor bajo si la variabilidad de la variable ‘Inversión’ en la muestra fuese muy elevada. En cuyo caso, t_{1} tomaría un valor elevado y su probabilidad asociada sería pequeña. 

Pregunta 5

c. La existencia de un elevado grado de multicolinealidad no supone el incumplimeinto de la hipótesis de rango pleno.

Pregunta 6

a. Al existir un elevado grado de multicolinealidad, hay dificultades para interpretar los coeficientes estimados porque no es posible suponer que las restantes explicativas del modelo permanecen constantes.

c. Aunque en el modelo exista un elevado grado de multicolinealidad no se incumple ninguna de las hipótesis del MRLNC por lo que los EMCO(b) son lineales, insesgados, óptimos, los más eficientes entre los ELI y consistentes.

Pregunta 7

b. Si existe un elevado grado de multicolinealidad los EMCO son insesgados y consistentes.

Pregunta 8

c. Aunque en el modelo exista un elevado grado de multicolinealidad no se incumple ninguna de las hipótesis del MRLNC.

d. S^2_{b_{2}} =\frac {S^{2}}{\sum{(PU_{t} – \overline{PU})^{2} (1-R^{2}_{PU})}} toma un valor bajo si la variabilidad de la variable ‘Índice de precios de coches usados’ en la muestra es elevada. 

Pregunta 9

a. Aunque en el modelo exista un elevado grado de multicolinealidad no se incumple ninguna de las hipótesis del MRLNC. Los EMCO(b) siguen siendo lineales, insesgados, óptimo, los más eficientes entre los ELI y consistentes.

b. Al existir un elevado grado de multicolinealidad, hay dificultad para interpretar los coeficientes estimados porque no es posible suponer que las restantes explicativas del modelo permanecen constantes.

Pregunta 10

c. S^2_{b_{3}} =\frac {S^{2}}{\sum{(NSD_{t} – \overline{NSD})^{2} (1-R^{2}_{NSD})}} toma un valor elevado si la variabilidad de la variable ‘Índice de precios de coches usados’ en la muestra fuese escasa.

d. Aunque en el modelo exista un elevado grado de multicolinealidad no se incumple ninguna de las hipótesis del MRLNC. Los EMCO(b) siguen siendo lineales, insesgados, óptimos, los más eficientes entre los ELI y consistentes.

Pregunta 11

b. Aunque en el modelo exista un elevado grado de multicolinealidad no se incumple la hipótesis de rango pleno.

d. Aunque en el modelo exista un elevado grado de multicolinealidad no se incumple ninguna de las hipótesis del MRLNC. Las varianzas estimadas de los estimadores son estimadores insesgados de las varianzas poblacionales de los estimadores — E(S^2_{b_{i}})= \sigma^2_{b_{i}}—

Pregunta 12

a. S^2_{b_{1}} =\frac {S^{2}}{\sum{(R_{t} – \overline{R})^{2} (1-R^{2}_{R})}} toma un valor bajo si la variabilidad de la variable ‘Renta disponible per cápita’ en la muestra es elevada.

b. Al existir un elevado grado de multicolinealidad, no es posible suponer que las restantes explicativas del modelo permanecen constantes.